
| A. | ①③ | B. | ②③ | C. | ②④ | D. | ③④ |
分析 判断对于函数f(x)为准奇函数的主要标准是:若存在常数a≠0,函数f(x)的图象关于(a,0)对称,则称f(x)为准奇函数.
解答 解:对于函数f(x),若存在常数a≠0,使得x取定义域内的每一个值,都有f(x)=-f(2a-x)知,
函数f(x)的图象关于(a,0)对称,
①函数的定义域为[0,+∞),函数为增函数,则函数不存在对称中心,所以①不是准奇函数.
②若f(x)=-f(2a-x),则ex=-e(2a-x),
∵ex>0,-e(2a-x)<0,∴ex=-e(2a-x),无解所以②不是准奇函数
③f(x)=cos(x+1)存在对称中心,所以③是准奇函数
④f(x)=tanx存在对称中心,则④为准奇函数,
故选:D.
点评 本题考查新定义的理解和应用,根据条件得到函数f(x)的图象关于(a,0)对称,则称f(x)为准奇函数是关键.


科目:高中数学 来源: 题型:选择题
| A. | y=sin$\frac{x}{2}$ | B. | y=cos2x | C. | y=sin(2x+$\frac{π}{4}$) | D. | y=tan(x-$\frac{π}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | an=$\frac{1}{n+1}$ | B. | an=$\frac{1}{2}$+$\frac{n-1}{{n}^{2}+n+2}$ | ||
| C. | an=$\frac{n+1}{n+2}$ | D. | an=$\frac{n}{n+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
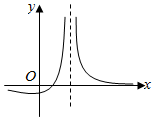 函数f(x)=$\frac{ax-b}{{{{(x-c)}^2}}}$的图象如图所示,则下列结论成立的是( )
函数f(x)=$\frac{ax-b}{{{{(x-c)}^2}}}$的图象如图所示,则下列结论成立的是( )| A. | a>0,b>0,c>0 | B. | a<0,b<0,c>0 | C. | a>0,b>0,c<0 | D. | a<0,b>0,c>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com