
| A. | y=3x+1 | B. | y=2-x-2x | C. | y=x2+1 | D. | y=x|x| |
分析 根据奇函数图象的对称性,一次函数的图象,减函数、增函数的定义,偶函数、奇函数的定义,二次函数的单调性即可判断每个选项的正误,从而找到正确选项.
解答 解:A.y=3x+1,该函数的图象既不关于y轴对称,也不关于原点对称,∴该函数为非奇非偶函数,∴该选项错误;
B.y=2-x-2x,x增大时,y减小,∴该函数为减函数,∴该选项错误;
C.y=x2+1,显然该函数为偶函数,∴该选项错误;
D.y=x|x|,显然该函数为奇函数,y=x|x|=$\left\{\begin{array}{l}{{x}^{2}}&{x≥0}\\{-{x}^{2}}&{x<0}\end{array}\right.$,而x≥0时,x2递增,x<0时,-x2递增,且x<0时,-x2<0;
∴函数y=x|x|是增函数;
∴该选项正确.
故选:D.
点评 考查奇函数图象的对称性,奇函数、偶函数的定义,能画出一次函数的定义,函数单调性的定义,以及二次函数的单调性,分段函数的单调性.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 16 | C. | 12 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
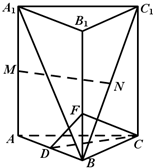 如图所示,在直三棱柱ABC-A1B1C1中,D、M、N分别是AB、AA1、BC1的中点.
如图所示,在直三棱柱ABC-A1B1C1中,D、M、N分别是AB、AA1、BC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $±\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{3}}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com