
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
分析 根据互为逆否命题的真假一致,将判断“a≠1或b≠3”是“a•b≠3”成立的什么条件转换为判断a•b=3是a=1且b=3成立的什么条件.
解答 解:由题意得:
∵命题若a≠1或b≠3则a•b≠3与命题若a•b=3则a=1且b=3互为逆否命题,
因为当a=$\frac{1}{2}$,b=6有a•b=3,
所以“命题若a•b=3则a=1且b=3”显然是假命题,
所以命题若a≠1或b≠,3则a•b≠3是假命题,
所以a≠1或b≠3推不出a•b≠3,不是充分条件;
“若a=1且b=3则a•b=3”是真命题,
∴命题若a•b≠3则≠1或b≠3是真命题,
∴a•b≠3⇒a≠1或b≠3,是必要条件,
“a≠1或b≠3”是“a•b≠3”的必要不充分条件.
故选:B.
点评 判断充要条件时可以先判断某些命题的真假,当命题的真假不易判断时可以先判断原命题的逆否命题的真假(原命题与逆否命题的真假相同).


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $±\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
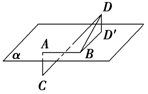 如图所示,已知线段AB在平面α内,线段AC⊥α,线段BD⊥AB,线段DD′⊥α于D′,如果∠DBD=30°,AB=AC=BD=1,则CD的长为2.
如图所示,已知线段AB在平面α内,线段AC⊥α,线段BD⊥AB,线段DD′⊥α于D′,如果∠DBD=30°,AB=AC=BD=1,则CD的长为2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com