
| A. | ①② | B. | ②③ | C. | ①④ | D. | ②④ |
分析 根据抛物线的性质,可判断①;写出原命题的逆命题,可判断②;根据回归系数的几何意义,可判断③;根据对立事件概率减法公式,求出甲胜的概率,可判断④
解答 解:①抛物线x2=4y的准线方程为y=-1,故①为真命题;
②命题“若x2+y2=0,则x=y=0”的逆命题是“若x=y=0,则x2+y2=0”为真命题;
③已知人体脂肪含量的百分比y与年龄x(岁)之间的线性回归方程为$\widehat{y}$=0.6x-0.5,若某人的年龄每增长一岁,则其脂肪含量的百分比平均增长0.6,故③为假命题;
④甲、乙两人下棋,和棋的概率为$\frac{1}{3}$,乙胜的概率为$\frac{1}{2}$,则甲胜的概率为$\frac{1}{6}$,故④为假命题;
故真命题的序号是①②,
故选:A.
点评 本题以命题的真假判断为载体,考查了抛物线的性质,四种命题;回归系数,概率等知识点,难度不大,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
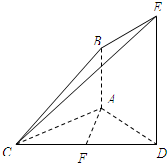 如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2AB,F是CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2AB,F是CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com