
分析 (1)利用函数是奇函数,函数值列出方程,即可求出a,b.
(2)直接利用函数的单调性的定义证明即可.
解答 解:(1)∵f(x)为R上奇函数,∴f(0)=0,
即a=-b①
∵$f(1)=\frac{2a+b}{3}=\frac{1}{3}$,
∴2a+b=1,②
结合①②有 a=1,b=-1…(6分)
(2)由(1)得$f(x)=\frac{{{2^x}-1}}{{{2^x}+1}}=1-\frac{2}{{{2^x}+1}}$,
设x1<x2则${2^{x_1}}<{2^{x_2}},f({x_1})-f({x_2})=\frac{2}{{{2^{x_2}}+1}}-\frac{2}{{{2^{x_1}}+1}}=\frac{{2({2^{x_1}}-{2^{x_2}})}}{{({2^{x_2}}+1)({2^{x_1}}+1)}}<0$,
即f(x1)<f(x2),
∴f(x)为单调递增函数. …(12分)
点评 本题考查函数的奇偶性以及单调性的判断与应用,考查函数与方程的思想,是基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | y=x${\;}^{\frac{1}{3}}$ | B. | y=log${\;}_{\frac{1}{3}}$|x| | C. | y=x+$\frac{2}{x}$ | D. | y=2-x-2x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 无数个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8毫克 | B. | 16毫克 | C. | 32毫克 | D. | 64毫克 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
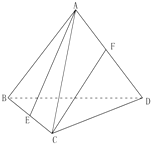 如图,在正四面体ABCD(正四面体是所有棱长都相等的四面体)中,棱长为2,E、F分别为BC、AD的中点.
如图,在正四面体ABCD(正四面体是所有棱长都相等的四面体)中,棱长为2,E、F分别为BC、AD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com