
分析 (Ⅰ)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;(Ⅱ)通过讨论a的范围,结合函数的单调性以及取特殊值方法求出a的具体范围即可.
解答 解:(Ⅰ)$f'(x)=a{e^{ax}}\frac{(x+1)[(a+1)x-1]}{x^2}$
①当a=-1时,令f′(x)=0,解得 x=-1,
f(x)的单调递减区间为(-∞,-1);单调递增区间为(-1,0),(0,+∞);
当a≠-1时,令f′(x)=0,解得 x=-1,或$x=\frac{1}{a+1}$,
②当-1<a<0时,f(x)的单调递减区间为(-∞,-1),$(\frac{1}{a+1},+∞)$
单调递增区间为(-1,0),$(0,\frac{1}{a+1})$;
③当a=0时,f(x)为常值函数,不存在单调区间;
④当a>0时,f(x)的单调递减区间为(-1,0),$(0,\frac{1}{a+1})$,
单调递增区间为(-∞,-1),$(\frac{1}{a+1},+∞)$;
(Ⅱ)①当a>0时,若x∈(0,+∞),
$f{(x)_{min}}=f(\frac{1}{a+1})={e^{\frac{a}{a+1}}}{(a+1)^2}>1$,
若x∈(-∞,0),$f{(x)_{max}}=f(-1)={e^{-a}}<1$,不合题意;
②当a=0时,显然不合题意;
③当-1<a<0时,取${x_1}=-\frac{a}{2}$,则$f({x_1})={e^{-\frac{a^2}{2}}}(a-1)<0$,
取x2=-1,则$f({x_2})={e^{-a}}>0$,符合题意;
④当a=-1时,取x1=1,则$f({x_1})=-{e^{-1}}<0$,
取x2=-1,则$f({x_2})={e^{-a}}>0$,符合题意;
综上,a的取值范围是[-1,0).
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | y2=12x | B. | y2=14x | C. | y2=16x | D. | y2=18x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
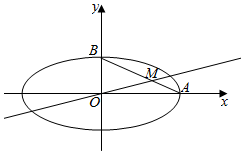 如图,椭圆E的方程为$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),点O为坐标原点,点A,B分别是椭圆的右顶点和上顶点,点M在线段AB上,满足BM=2MA,直线OM的斜率为$\frac{1}{4}$.
如图,椭圆E的方程为$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),点O为坐标原点,点A,B分别是椭圆的右顶点和上顶点,点M在线段AB上,满足BM=2MA,直线OM的斜率为$\frac{1}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ex•sin2x+ex•cos2x | B. | ex•sin2x+2ex•cos2x | ||
| C. | ex•sin2x-ex•cos2x | D. | ex•sin2x-2ex•cos2x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 家庭月收入 (单位:元) | 2千以下 | 2千~5千 | 5千~8千 | 8千~一万 | 1万~2万 | 2万以上 |
| 调查的总人数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 有二孩计划的家庭数 | 1 | 2 | 9 | 7 | 3 | 4 |
| 收入不高于8千的家庭数 | 收入高于8千的家庭数 | 合计 | |
| 有二孩计划的家庭数 | |||
| 无二孩计划的家庭数 | |||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com