
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | 2π | $\frac{13π}{2}$ | |||
| f(x) | 0 | 4 | -4 | 0 |
分析 (1)根据表中数据求出A、T以及ω和φ的值,写出f(x)的解析式,再补充表中数据;
(2)根据函数图象变换写出g(x)的解析式,求出它在区间[π,$\frac{5π}{2}$]上的最值即可.
解答 解:(1)根据表中数据得,A=4,
$\frac{3}{4}$T=$\frac{13π}{2}$-2π=$\frac{9π}{2}$,
所以T=6π=$\frac{2π}{ω}$,
解得ω=$\frac{1}{3}$,
所以$\frac{1}{3}$×$\frac{π}{2}$+φ=0,
解得φ=-$\frac{π}{6}$;
所以$f(x)=4sin(\frac{1}{3}x-\frac{π}{6})$,
补充表中数据为$\frac{π}{2}$,$\frac{7π}{2}$,5π和0;
(2)将函数f(x)的图象上每一点的纵坐标缩短到原来的$\frac{1}{2}$倍,横坐标不变,
得到函数g(x)的图象,
所以$g(x)=2sin(\frac{1}{3}x-\frac{π}{6})$,
∵$π≤x≤\frac{5π}{2}$,
∴$\frac{π}{6}≤\frac{1}{3}x-\frac{π}{6}≤\frac{2π}{3}$,
∴$\frac{1}{2}≤sin(\frac{1}{3}x-\frac{π}{6})≤1$,
∴$1≤2sin(\frac{1}{3}x-\frac{π}{6})≤2$,
∴g(x)max=2,g(x)min=1.
点评 本题考查了三角函数f(x)=Asin(ωx+φ)的图象与性质的应用问题,也考查了图象的变换问题,是基础题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
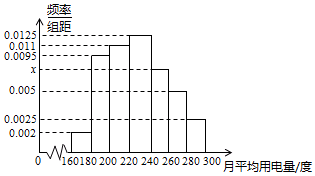 某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.
某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com