Question

2．若满足$\left\{\begin{array}{l}{2x-y+1≥0}\\{x+2y-2≥0}\\{ax+by+c≤0}\end{array}\right.$，的点（x，y）所表示的区域能被直径为$\sqrt{10}$的圆完全覆盖，则区域D的面积最大值为$\frac{5}{2}$，当区域D的面积最大时，z=x-y最大值为2．

Answer 1

分析 由题意作平面区域，易知BC⊥BA，从而可得当三角形内接于圆时，面积最大，从而求最大值及点A的坐标，从而求得．

解答 解：由题意作平面区域如下，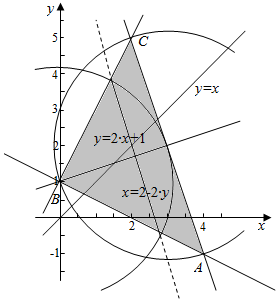

易知直线y=2x+1与直线x=2-2y互相垂直，即BC⊥BA；
故当三角形内接于圆时，面积最大，
故区域D的面积最大值为$\frac{1}{2}$×$\sqrt{10}$×$\frac{\sqrt{10}}{2}$=$\frac{5}{2}$，
故设A（2-2y，y），
|BA|=$\sqrt{（2-2y）^{2}+（y-1）^{2}}$=$\frac{\sqrt{10}}{\sqrt{2}}$，
解得，y=0或y=2（舍去）；
故A（2，0），
故 z=x-y最大值为2-0=2，
故答案为：$\frac{5}{2}$，2．

点评 本题考查了线性规划的变形应用及数形结合的思想方法应用，属于中档题．