
分析 (1)根据递推公式,代值计算即可,
(2)根据an+1=Sn+1-Sn,求得an+1+3=2(an+3),判断出数列{an+3}是等比数列,
(3)利用等比数列的通项公式求得an+3进而求得an.
(4)设存在s,p,r∈N*,且s<p<r,使得as,ap,ar成等差数列,根据等差中项的性质可知2ap=as+ar,利用(1)中的an展开得2p+1=2s+2r,2p-s+1=1+2r-s,进而根据2p-s+1,2r-s为偶数,而1+2r-s为奇数,判断出假设不成立.故可知不存在这样的三项.
解答 解:(1)因为Sn=2an-3n,
当n=1时,S1=2a1-3,解得a1=3,
当n=2时,S2=2a2-3,解得a2=6,
(2)因为Sn=2an-3n,
所以Sn+1=2an+1-3(n+1),
则an+1=2an+1-2an-3,
所以an+1=2an+3,
所以an+1+3=2(an+3)
数列{an+3}是等比数列,
(3)由(2)知,数列{an+3}是等比数列,
因为a1+3=6,
所以an+3=6•2n-1=3•2n,
所以an=3•2n-3.
(4)设存在s,p,r∈N*,且s<p<r,使得as,ap,ar成等差数列,
则2ap=as+ar,即2(3•2p-3)=3•2s-3+3•2r-3
即2p+1=2s+2r,2p-s+1=1+2r-s,2p-s+1,2r-s为偶数,而1+2r-s为奇数,
所以2p+1=2s+2r不成立,故不存在满足条件的三项.
点评 题考查数列的通项公式的求法,探索数列{an}中是否存在三项成等差数列.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}\sqrt{3}$ | B. | $\frac{4}{3}\sqrt{2}$ | C. | $\frac{4}{3}\sqrt{6}$ | D. | $\frac{2}{3}\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
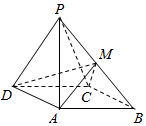 如图,四棱锥P-ABCD中,侧面PDC是正三角形,底面ABCD是边长为$2\sqrt{3}$的菱形,∠DAB=120°,且侧面PDC与底面垂直,M为PB的中点.
如图,四棱锥P-ABCD中,侧面PDC是正三角形,底面ABCD是边长为$2\sqrt{3}$的菱形,∠DAB=120°,且侧面PDC与底面垂直,M为PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{8}$ | B. | 2 | C. | 6 | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com