
| A. | f(x)有三个零点,且所有零点之积大于-1 | |
| B. | f(x)有三个零点,且所有零点之积小于-1 | |
| C. | f(x)有四个零点,且所有零点之积大于1 | |
| D. | f(x)有四个零点,且所有零点之积小于1 |
分析 函数f(x)是一个对数函数减去一个指数函数.由绝对值的性质知,
解答 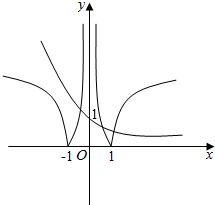 解:对数函数y=|log2|x||的图象是对数函数y=log2x的图象将x轴下侧图象翻到x轴上方之后再关于y轴对称得到.
解:对数函数y=|log2|x||的图象是对数函数y=log2x的图象将x轴下侧图象翻到x轴上方之后再关于y轴对称得到.
其函数图象与指数函数y=${(\frac{1}{2})}^{x}$的图象有3个交点,所以函数f(x)有3个零点.
∵|${log}_{2}\frac{1}{\sqrt{2}}$|=$\frac{1}{2}$,${log}_{2}\sqrt{2}$=$\frac{1}{2}$
而${(\frac{1}{2})}^{1}$=$\frac{1}{2}$,
∴对数函数y=|log2|x||与指数函数y=${(\frac{1}{2})}^{x}$的两个交点分别在(0,$\frac{1}{\sqrt{2}}$)与(1,$\sqrt{2}$)之间,
这两个交点的乘积小于$\frac{1}{\sqrt{2}}×\sqrt{2}$=1
而第三个交点在(-$\frac{1}{2}$,0)之间,
∴三个交点的积小于-1.
即函数f(x)的3个零点的积小于-1
故选:B.
点评 本题考查的是将一个复杂函数求零点问题转化为对数函数与指数函数图象相交的交点问题.而且对函数绝对值问题也需熟练掌握.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:选择题
| A. | y2=8x | B. | x2=4y | C. | y2=8x或x2=-4y | D. | y2=8x或x2=4y |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com