考点:命题的真假判断与应用
专题:平面向量及应用,空间向量及应用
分析:A.由
•=0,利用数量积定义可得∠BAC=90°,即△ABC为直角三角形,反之不成立;
B.由
=+,可知
+≠1,利用向量共线定理即可判断出;
C.利用基底的意义即可判断出;
D.左边=
|| || |cos<,>| ||,右边=
|| || ||,即可判断出.
解答:
解:A.由
•=0⇒
|| ||cos∠BAC=0⇒cos∠BAC=0⇒∠BAC=90°,即△ABC为直角三角形.
反之不成立,因此
•=0是△ABC为直角三角形的充分不必要条件,因此不正确;
B.∵
=+,可知
+≠1,因此P、A、B三点不共线,因此不正确;
C.假设存在实数满足
+=λ(+)+μ(+),化为
(λ-1)+(λ+μ)+(μ-1)=,
∵
{,,}为空间的一个基底,∴
,此方程组无解,因此假设不成立.
∴
{+,+,+}也构成空间的一个基底,因此正确.
D.左边=
|| || |cos<,>| ||,右边=
|| || ||,
因此左边=右边不恒成立,故不正确.
综上可知:只有D正确.
故选:D.
点评:本题综合考查了数量积的意义、空间向量的基底、向量共线定理等基础知识与基本技能方法,属于中档题.



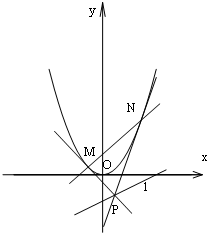 已知抛物线C:y=x2,直线l:x-2y-2=0,点P是直线l上任意一点,过点P作抛物线C的切线PM,PN,切点分别为M,N,直线PM,PN斜率分别为k1,k2,如图所示.
已知抛物线C:y=x2,直线l:x-2y-2=0,点P是直线l上任意一点,过点P作抛物线C的切线PM,PN,切点分别为M,N,直线PM,PN斜率分别为k1,k2,如图所示.