
分析 可作出图形,由图形可看出$\overrightarrow{FP}•\overrightarrow{FQ}=|\overrightarrow{FQ}{|}^{2}-1$,而根据抛物线的定义,|FQ|等于Q到抛物线C的准线y=-2的距离,根据图形便可看出Q到准线的最短距离为2,从而便可得出$\overrightarrow{FP}•\overrightarrow{FQ}$的最小值为3.
解答 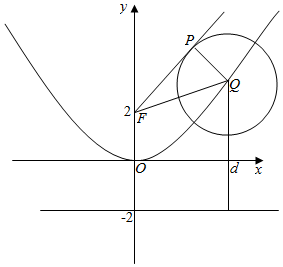 解:如图,$\overrightarrow{FP}•\overrightarrow{FQ}={|{\overrightarrow{FP}}|^2}={|{\overrightarrow{FQ}}|^2}-{r^2}={|{\overrightarrow{FQ}}|^2}-1$;
解:如图,$\overrightarrow{FP}•\overrightarrow{FQ}={|{\overrightarrow{FP}}|^2}={|{\overrightarrow{FQ}}|^2}-{r^2}={|{\overrightarrow{FQ}}|^2}-1$;
由抛物线的定义知:$|{\overrightarrow{FQ}}|=d,d$为点Q到准线的距离,易知,抛物线的顶点到准线的距离⑥最短,${|{\overrightarrow{FQ}}|_{min}}=2$;
∴${(\overrightarrow{FP}•\overrightarrow{FQ})_{min}}=3$;
即$\overrightarrow{FP}•\overrightarrow{FQ}$的最小值为3.
故答案为:3.
点评 考查圆心和切点连线垂直于切线,余弦函数的定义,直角三角形边的关系,以及抛物线的定义,抛物线的标准方程,抛物线的焦点和准线,以及数形结合解题的方法.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{5}{3}$ | C. | $\frac{4}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p是真命题 | B. | 命题p的逆命题是真命题 | ||
| C. | 命题p的否命题是:若a<1,则a2≥1 | D. | 命题p的逆否命题是:若a2≥1,则a<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
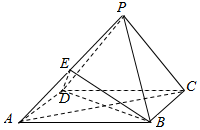 如图,在四棱锥P-ABCD中,底面为矩形,平面PCD丄平面ABCD,PC丄PD,PD=AD,E为PA的中点.
如图,在四棱锥P-ABCD中,底面为矩形,平面PCD丄平面ABCD,PC丄PD,PD=AD,E为PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 3或5 | D. | 4或5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com