Question

8．四棱锥P-ABCD中，底面ABCD是边长为2的菱形，∠ABC=60°，E为AB的中点，PA⊥平面ABCD，PC与平面PAD所成的角的正弦值为$\frac{{\sqrt{6}}}{4}$．
（1）在棱PD上求一点F，使AF∥平面PEC；
（2）求二面角D-PE-A的余弦值．

Answer 1

分析 （1）分别取PD，PC的中点F，G，由三角形中位线定理及平行公理可得四边形AEGF为平行四边形，得AF∥EG，由线面平行的判定可得AF∥平面PEC，则PD的中点F即为所求；
（2）由已知可得∠CPE即为PC与平面PAB所成的角，求解直角三角形得到PA=2，过D作BA的延长线的垂线，垂足为H，过H作PE的垂线，垂足为K，连接KD，可得∠DKH即为所求的二面角的平面角，然后求解直角三角形得答案．

解答 解：（1）分别取PD，PC的中点F，G，则FG∥CD∥AB，$FG=\frac{1}{2}CD=\frac{1}{2}AB=AE$，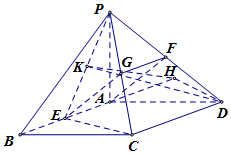
∴四边形AEGF为平行四边形，则AF∥EG，又FG?平面PEC，
∴AF∥平面PEC，
∴PD的中点F即为所求；
（2）由PA⊥平面ABCD，可得平面PAB⊥平面ABCD，
∵E为AB中点，且BC=2BE=2，∠CBE=60°，∴CE⊥AB．
∴∠CPE即为PC与平面PAB所成的角，
在Rt△PEC中，$\frac{CE}{CP}=\frac{{\sqrt{6}}}{4}$，即$\frac{{\sqrt{3}}}{{\sqrt{3+1+P{A^2}}}}=\frac{{\sqrt{6}}}{4}$，
解得：PA=2，
过D作BA的垂线，垂足为H，过H作PE的垂线，垂足为K，连接KD，
∵PA⊥平面ABCD，∴PA⊥DH，
又DH⊥BA，∴DH⊥平面PBA，
∴DH⊥PE，则PE⊥平面DHK，得PE⊥DH，
∴∠DKH即为所求的二面角的平面角，
在Rt△DHK中，$DH=\sqrt{3}$，
由于PE•HK=EH•PA，∴$HK=\frac{EH•PA}{PE}=\frac{4}{{\sqrt{5}}}$，
从而$DK=\sqrt{3+\frac{16}{5}}=\sqrt{\frac{31}{5}}$，
∴$cos∠DKH=\frac{KH}{DK}=\frac{{4\sqrt{31}}}{31}$，
即二面角D-PE-A的余弦值为$\frac{{\sqrt{2}}}{2}$．

点评 本题考查线面平行的判定，考查了二面角平面角的求法，正确找出二面角的平面角是解答该题的关键，是中档题．