
| A. | (1,3) | B. | (0,3) | C. | (0,2) | D. | (0,1) |
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:高中数学 来源:2017届陕西汉中城固县高三10月调研数学(文)试卷(解析版) 题型:选择题
设 是函数
是函数 定义域内的一个区间,若存在
定义域内的一个区间,若存在 ,使得
,使得 ,则称
,则称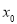 是
是 的一个“次不动点”,也称
的一个“次不动点”,也称 在区间
在区间 上存在次不动点.若函数
上存在次不动点.若函数 在区间
在区间 上存在次不动点,则实数
上存在次不动点,则实数 的取值范围是( )
的取值范围是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{5}$ | B. | $\frac{8}{5}$ | C. | 1 | D. | $\frac{29}{15}$ |
查看答案和解析>>
科目:高中数学 来源:2017届陕西汉中城固县高三10月调研数学(理)试卷(解析版) 题型:解答题
“健步走”是一种方便而又有效的锻炼方式,李老师每天坚持“健步走”,并用计步器进行统计.他最近8天“健步走”步数的条形统计图及相应的消耗能量数据表如下:


(1)求李老师这8天“健步走”步数的平均数;
(2)从步数为16千步,17千步,18千步的6天中任选2天,设李老师这2天通过“健步走”消耗的能量和为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -35°+k•360°,k∈Z | B. | -325°+k•360°,k∈Z | ||
| C. | 325°+k•360°,k∈Z | D. | 35°+(2k+1)×180°,k∈Z |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com