
| A. | [-2,0] | B. | [-1,0] | C. | [0,1] | D. | [0,2] |
分析 由题意可得g′(x)=exf(x)+exf′(x)=2x,得到g(x)=x2+c(其中c为常数),进一步可得f(x)=$\frac{{x}^{2}+c}{{e}^{x}}$,结合f(0)=1求得c=1,得到f(x)的解析式,求导后可得$\frac{f′(x)}{f(x)}=\frac{2x-{x}^{2}-1}{{x}^{2}+1}=-1+\frac{2x}{{x}^{2}+1}$,然后对x分类求得函数$\frac{f′(x)}{f(x)}$的取值范围.
解答 解:由f′(x)+f(x)=2xe-x,
得$\frac{f′(x)+f(x)}{{e}^{-x}}=2x$,即exf′(x)+exf(x)=2x,
令g(x)=exf(x),则g′(x)=exf(x)+exf′(x)=2x,
∴g(x)=x2+c(其中c为常数),
∴f(x)=$\frac{{x}^{2}+c}{{e}^{x}}$,
又f(0)=1,
∴c=1,则f(x)=$\frac{{x}^{2}+1}{{e}^{x}}$,
∴f′(x)=$\frac{2x-{x}^{2}-1}{{e}^{x}}$,
∴$\frac{f′(x)}{f(x)}=\frac{2x-{x}^{2}-1}{{x}^{2}+1}=-1+\frac{2x}{{x}^{2}+1}$,
当x=0时,$\frac{f′(x)}{f(x)}=-1$,
当x≠0时,$\frac{f′(x)}{f(x)}=-1+\frac{2}{x+\frac{1}{x}}$,
∵$x+\frac{1}{x}∈(-∞,-2]∪[2,+∞)$,
∴$\frac{f′(x)}{f(x)}$∈[-2,0].
故选:A.
点评 本题考查导数的运算,考查了数学转化思想方法,考查了函数构造法,训练了利用基本不等式求函数的最值,题目设置难度较大.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
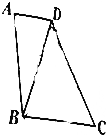 在直角梯形ABCD中,AD∥BC,∠A=90°,AB=2AD,若将△ABD沿直线BD折成△A′BD,使得A′D⊥BC,则直线A′B与平面BCD所成角的正弦值是$\frac{\sqrt{3}}{4}$.
在直角梯形ABCD中,AD∥BC,∠A=90°,AB=2AD,若将△ABD沿直线BD折成△A′BD,使得A′D⊥BC,则直线A′B与平面BCD所成角的正弦值是$\frac{\sqrt{3}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 16 | C. | 12 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com