Question

9．如图，四边形ABCD是正方形，PA⊥平面ABCD，PA=AB
（1）求证：PC⊥BD；
（2）求PC与平面ABCD所成角的余弦值．

Answer 1

分析 （1）连结AC，通过证明BD⊥平面PAC得出BD⊥PC；
（2）∠PCA为所求的线面角，设AB=PA=a，利用勾股定理计算出AC，PC即可解出．

解答 证明：（1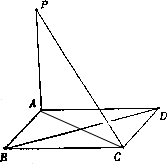）连结AC．
∵四边形ABCD是正方形，
∴BD⊥AC．
∵PA⊥平面ABCD，BD?平面ABCD，
∴PA⊥BD．
又PA?平面PAC，AC?平面PAC，PA∩AC=A，
∴BD⊥平面PAC，∵PC?平面PAC，
∴BD⊥PC．
（2）∵PA⊥平面ABCD，
∴∠PCA为直线PC与平面ABCD所成的角，
设PA=AB=a，
∵四边形ABCD是正方形，∴AC=$\sqrt{2}$AB=$\sqrt{2}a$．
∴PC=$\sqrt{P{A}^{2}+A{C}^{2}}$=$\sqrt{3}a$，
∴cos∠PCA=$\frac{AC}{PC}$=$\frac{\sqrt{2}a}{\sqrt{3}a}=\frac{\sqrt{6}}{3}$．

点评 本题考查了线面垂直的判定与性质，线面角的计算，属于基础题．