
分析 (1)当m=3,n=1时,不等式f(x)>3可化为-x2-3x-2>0,即可求不等式f(x)>3的解集;
(2)由两个零点分别在区间(-1,2)和(2,3)内,根据零点存在定理,我们易得:f(-1)<0,f(2)>0,f(3)<0,由此我们易构造一个平面区域,利用线性规划知识即可求出答案.
(3)确定n=-2m,$\frac{m}{a-1}$≤1,利用韦达定理,即可证明.
解答 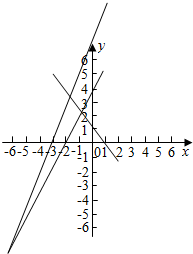 解:(1)当m=3,n=1时,不等式f(x)>3可化为-x2-3x-2>0,∴-2<x<-1,
解:(1)当m=3,n=1时,不等式f(x)>3可化为-x2-3x-2>0,∴-2<x<-1,
∴不等式f(x)>3的解集(-2,-1);
(2)∵函数f(x)=-x2-mx+n(m,n∈R)的两个零点分别在区间(-1,2)和(2,3)内,
∴f(-1)<0,f(2)>0,f(3)<0,
∴$\left\{\begin{array}{l}{-1+m+n<0}\\{-4-2m+n>0}\\{-9-3m+n<0}\end{array}\right.$,
平面区域如图所示,三个交点坐标分别为(-1,2),(-2,3),(-5,-6),
∴m+2n在(-2,3)处取得最大值4,在(-5,-6)处取得最小值为-17,
∴m+2n的取值范围为(-17,4).
(3)h(x)=(a-1)x2-mx+n,
∵f(-2)=-4,且h(-1)•h(1)≤0,
∴2m+n=0,(a-1+m+n)(a-1-m+n)≤0,
∴n=-2m,$\frac{m}{a-1}$≤1
h(x)=(a-1)x2-mx+n=0,x1+x2=$\frac{m}{a-1}$,x1x2=$\frac{n}{a-1}$=-$\frac{2m}{a-1}$,
|x1-x2|=$\sqrt{(\frac{m}{a-1}+4)^{2}-16}$,∴$\frac{m}{a-1}$=1,即m=a-1时,|x1-x2|取得最大值.
点评 本题考查二次函数的性质,函数零点的求法及零点存在定理,其中连续函数在区间(a,b)满足f(a)•f(b)<0,则函数在区间(a,b)有零点,是判断函数零点存在最常用的方法.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -cos160° | B. | cos160° | C. | $\frac{1}{cos160°}$ | D. | $\frac{1}{-cos160°}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2个球都是白球的概率 | B. | 2个球中恰好有1个是白球的概率 | ||
| C. | 2个球都不是白球的概率 | D. | 2个球至少有一个白球的概率 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{π}{4}$,$\frac{2π}{3}$] | B. | [-$\frac{π}{8}$,$\frac{π}{4}$] | C. | [-$\frac{π}{8}$,$\frac{2π}{3}$] | D. | [0,$\frac{2π}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在△ABC中,AC=$\sqrt{2}$,AB=$\sqrt{3}$+1,∠BAC=45°,点P满足:$\overrightarrow{BP}$=(1-λ)$\overrightarrow{BA}$+λ$\overrightarrow{BC}$(λ>0),AP=$\frac{\sqrt{2}}{2}$.
在△ABC中,AC=$\sqrt{2}$,AB=$\sqrt{3}$+1,∠BAC=45°,点P满足:$\overrightarrow{BP}$=(1-λ)$\overrightarrow{BA}$+λ$\overrightarrow{BC}$(λ>0),AP=$\frac{\sqrt{2}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com