
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 分别写出命题p的逆命题、否命题和逆否命题,再判定它们的真假性.
解答 解:命题p中,$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{BA}$•$\overrightarrow{BC}$,
∴|$\overrightarrow{AB}$|×|$\overrightarrow{AC}$|cos∠CAB=|$\overrightarrow{BA}$|×|$\overrightarrow{BC}$|cos∠CBA,
∴|$\overrightarrow{AC}$|cos∠CAB=|$\overrightarrow{BC}$|cos∠CBA,即点C在底边AB上的射影是底边AB的中点,
∴|$\overrightarrow{AC}$|=|$\overrightarrow{BC}$|,p是真命题;
则命题p的逆命题是:“在△ABC中,若|$\overrightarrow{AC}$|=|$\overrightarrow{BC}$|,则$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{BA}$•$\overrightarrow{BC}$”,它是真命题;
∵|$\overrightarrow{AC}$|=|$\overrightarrow{BC}$|,∴|$\overrightarrow{AC}$|cos∠CAB=|$\overrightarrow{BC}$|cos∠CBA,
∴|$\overrightarrow{AB}$|×|$\overrightarrow{AC}$|cos∠CAB=|$\overrightarrow{BA}$|×|$\overrightarrow{BC}$|cos∠CBA,
即$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{BA}$•$\overrightarrow{BC}$,命题正确;
命题p的否命题是:“在△ABC中,若$\overrightarrow{AB}$•$\overrightarrow{AC}$≠$\overrightarrow{BA}$•$\overrightarrow{BC}$,则|$\overrightarrow{AC}$|≠|$\overrightarrow{BC}$|”,它是真命题;
命题p的逆否命题是:“在△ABC中,若|$\overrightarrow{AC}$|≠|$\overrightarrow{BC}$|,则$\overrightarrow{AB}$•$\overrightarrow{AC}$≠$\overrightarrow{BA}$•$\overrightarrow{BC}$”,它是真命题.
综上,命题p的逆命题、否命题、逆否命题中,真命题有3个.
故选:D.
点评 本题考查了四种命题之间的关系与应用问题,也考查了平面向量的数量积的应用问题,是综合性题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1<x<2} | B. | {x|x≥1} | C. | {x|x≤2} | D. | {x|x≤1或x≥2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
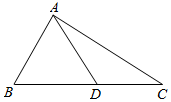 如图,在△ABC中,B=$\frac{π}{3}$,AC=$\sqrt{3}$,D为BC边上一点.若AB=AD,则△ADC的周长的取值范围为.
如图,在△ABC中,B=$\frac{π}{3}$,AC=$\sqrt{3}$,D为BC边上一点.若AB=AD,则△ADC的周长的取值范围为.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com