
分析 (Ⅰ)按照梦想函数的定义举反例即可;
(Ⅱ)求出h'(x)=cosx+a,由题意得h'(x)>h(x)在x∈[0,π]恒成立,即ax<cosx-sinx+1在x∈[0,π]上恒成立.x=0时易判断成立;当0<x≤π时,可得a<$\frac{cosx-sinx+1}{x}$对任意x∈(0,π]恒成立.令F(x)=$\frac{cosx-sinx+1}{x}$,利用导数可求得F(x)的最小值及其范围,从而得到a的范围,进而得到答案;
解答 解:(Ⅰ)函数f(x)=sinx不是其定义域上的梦想函数.
理由如下:f(x)=sinx的定义域D=R,f'(x)=cosx,
存在x=$\frac{π}{3}$,使f($\frac{π}{3}$)>f′($\frac{π}{3}$),
故函数h(x)=sinx不是其定义域D=R上的梦想函数.
(Ⅱ)h′(x)=cosx+a,由题意h'(x)>h(x)在x∈[0,π]恒成立,
故cosx+a>sinx+ax+a-1,即ax<cosx-sinx+1在x∈[0,π]上恒成立.
①当x=0时,a•0<cos0-sin0+1=2显然成立;
②当0<x≤π时,由ax<cosx-sinx+1,可得a<$\frac{cosx-sinx+1}{x}$对任意x∈(0,π]恒成立.
令F(x)=$\frac{cosx-sinx+1}{x}$,则F′(x)=$\frac{(-sinx-cosx)•x-(cosx-sinx+1)}{{x}^{2}}$,
令k(x)=(-sinx-cosx)•x-(cosx-sinx+1),
则k′(x)=(sinx-cosx)•x=$\sqrt{2}$x•sin(x-$\frac{π}{4}$),
当x∈(0,$\frac{π}{4}$]时,因为k'(x)≤0,所以k(x)在(0,$\frac{π}{4}$]单调递减;
当x∈($\frac{π}{4}$,π]时,因为k'(x)≥0,所以k(x)在($\frac{π}{4}$,π]单调递增.
∵k(0)=-2<0,k($\frac{π}{4}$)=-$\frac{\sqrt{2}}{4}$π-1<0,
∴当x∈(0,$\frac{π}{4}$]时,k(x)的值均为负数.
∵k($\frac{π}{4}$)=-$\frac{\sqrt{2}}{4}$π-1<0,k(π)=π>0,
∴当x∈($\frac{π}{4}$,π]时,k(x)有且只有一个零点x0,且x0∈($\frac{π}{4}$,π).
∴当x∈(0,x0)时,k(x)<0,所以F'(x)<0,可得F(x)在(0,x0)单调递减;
当x∈(x0,π)时,k(x)>0,所以F'(x)>0,可得F(x)在(x0,π)单调递增.
则F(x)min=F(x0)=$\frac{co{sx}_{0}-si{nx}_{0}+1}{{x}_{0}}$,
因为k(x0)=0,所以cosx0-sinx0+1=(-sinx0-cosx0)•x0,
F(x)min=F(x0)=-sinx0-cosx0=-$\sqrt{2}$sin(x0+$\frac{π}{4}$).
∵k(x)在($\frac{π}{4}$,π]上单调递增,k($\frac{π}{2}$)=-$\frac{π}{2}$<0,k($\frac{3π}{4}$)=$\sqrt{2}$-1>0,
∴$\frac{π}{2}$<x0<$\frac{3π}{4}$,
所以-1<-$\sqrt{2}$sin(x0+$\frac{π}{4}$)<0,即-1<F(x0)<0.
又因为a<F(x0),所以a的最大整数值为-1.
点评 本小题主要考查函数、导数等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、分类与整合思想、函数与方程思想、数形结合思想等.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
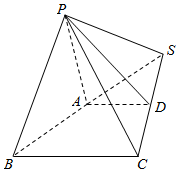 在三棱锥P-SBC中,A,D分别为边SB,SC的中点,且AB=3,BC=8,CD=5.PA⊥BC.
在三棱锥P-SBC中,A,D分别为边SB,SC的中点,且AB=3,BC=8,CD=5.PA⊥BC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
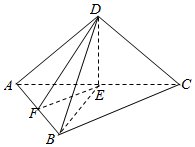 如图,在三棱锥D-ABC中,DA=DB=DC,D在底面ABC上的射影为E,AB⊥BC,DF⊥AB于F
如图,在三棱锥D-ABC中,DA=DB=DC,D在底面ABC上的射影为E,AB⊥BC,DF⊥AB于F查看答案和解析>>
科目:高中数学 来源: 题型:选择题
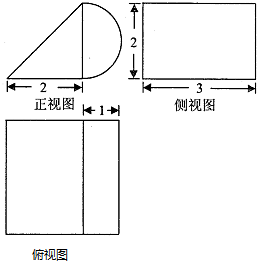
| A. | 4+$\frac{2}{3}π$ | B. | 4+$\frac{3}{2}$π | C. | 6+$\frac{2}{3}π$ | D. | 6+$\frac{3}{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com