
| 周一 | 周二 | 周三 | 周四 | 周五 | |
| 语文 | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{2}$ |
| 数学 | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{2}{3}$ |
| 外语 | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{2}{3}$ |
分析 (I)理解表格给出的数据,利用概率公式求解,P(A)=P($\overline{{A}_{1}}$$\overline{{A}_{2}}$$\overline{{A}_{3}}$)=(1-P(A))(1-P(B))(1-P(C));
(II)一周内有数学作业的天数为ξ,则ξ的所有可能取值为0、1、2、3、4、5,分别求解概率,分清事件的构成得出正确的概率,列出分布列.
解答 解:(Ⅰ)设周五有语文、数学、外语三科作业分别为事件A1、A2、A3周五没有语文、数学、外语三科作业为事件A,
则由已知表格得:P(A1)=$\frac{1}{2}$,P(A2)=$\frac{2}{3}$,P(A3)=$\frac{2}{3}$,P(A)=P($\overline{{A}_{1}}$$\overline{{A}_{2}}$$\overline{{A}_{3}}$)=(1-$\frac{1}{2}$)(1-$\frac{2}{3}$)(1-$\frac{2}{3}$);
(Ⅱ)设一周内有数学作业的天数为ξ,则ξ的所有可能取值为0、1、2、3、4、5,
∴P(ξ=0)=(1-$\frac{1}{2}$)4(1-$\frac{2}{3}$)=$\frac{1}{48}$
P(ξ=1)=${C}_{4}^{1}$$•\frac{1}{2}$(1-$\frac{1}{2}$)3(1-$\frac{2}{3}$)+(1-$\frac{1}{2}$)4(1-$\frac{2}{3}$)=$\frac{1}{8}$,
P(ξ=2)=${C}_{4}^{2}$($\frac{1}{2}$)2(1-$\frac{1}{2}$)2(1-$\frac{2}{3}$)+${C}_{4}^{1}$$•\frac{1}{2}$•(1-$\frac{1}{2}$)3$•\frac{2}{3}$=$\frac{7}{24}$
P(ξ=3)=${C}_{4}^{3}$•($\frac{1}{2}$)3(1-$\frac{1}{2}$)(1-$\frac{2}{3}$)+${C}_{4}^{2}$$•(\frac{1}{2})$2(1-$\frac{1}{2}$)2$•\frac{2}{3}$=$\frac{1}{3}$
P(ξ=4)=${C}_{4}^{4}$($\frac{1}{2}$)4(1-$\frac{2}{3}$)+${C}_{4}^{3}$×($\frac{1}{2}$)3(1-$\frac{1}{2}$)×$\frac{2}{3}$=$\frac{3}{16}$,
P(ξ=5)=($\frac{1}{2}$)4×$\frac{2}{3}$=$\frac{1}{24}$,
所以随机变量ξ的概率分布列如下:
| ξ | 0 | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{1}{48}$ | $\frac{1}{8}$ | $\frac{7}{24}$ | $\frac{1}{3}$ | $\frac{3}{16}$ | $\frac{1}{24}$ |
点评 本题考查了离散型的概率问题在实际问题中的应用,关键仔细阅读题意,弄清概率的类型,结构,熟练掌握好组合问题,属于难题.


科目:高中数学 来源: 题型:解答题
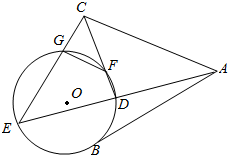 如图,AB是圆O的一条切线,切点为B,ADE,CFD,CGE都是圆O的割线,已知AC=AB.
如图,AB是圆O的一条切线,切点为B,ADE,CFD,CGE都是圆O的割线,已知AC=AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n•4n-1 | B. | 4n-1 | C. | n•2n-1+4n-1 | D. | n•4n-1+2n-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com