
分析 利用基本不等式可判断$\sqrt{ab}$<$\frac{a+b}{2}$,$\frac{a+b}{2}$<$\sqrt{\frac{{a}^{2}{+b}^{2}}{2}}$;利用不等式的性质可得a<$\frac{2ab}{a+b}$,$\sqrt{\frac{{a}^{2}{+b}^{2}}{2}}$<b,利用作差法判断$\frac{2ab}{a+b}$<$\sqrt{ab}$,从而确定大小顺序.
解答 解:∵b>a>0,
∴a<$\frac{2ab}{a+b}$,
∵$\sqrt{ab}$-$\frac{2ab}{a+b}$=$\frac{\sqrt{ab}}{a+b}$(a+b-2$\sqrt{ab}$)>0,
∴$\frac{2ab}{a+b}$<$\sqrt{ab}$,
易知$\sqrt{ab}$<$\frac{a+b}{2}$,
∵($\frac{a+b}{2}$)2<$\frac{{a}^{2}+{b}^{2}}{2}$,
∴$\frac{a+b}{2}$<$\sqrt{\frac{{a}^{2}{+b}^{2}}{2}}$,
故a<$\frac{2ab}{a+b}$<$\sqrt{ab}$<$\frac{a+b}{2}$<$\sqrt{\frac{{a}^{2}{+b}^{2}}{2}}$<b.
点评 本题考查了基本不等式及不等式的性质的应用,同时考查了作差法与演绎法的应用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
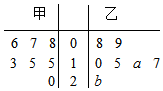 甲乙两家快餐店对某日7个时段来店光临的客人人数进行统计绘制茎叶图如图所示(下面简称甲数据、乙数据),且乙数据的众数为17,甲数据的平均数比乙数据平均数少2.
甲乙两家快餐店对某日7个时段来店光临的客人人数进行统计绘制茎叶图如图所示(下面简称甲数据、乙数据),且乙数据的众数为17,甲数据的平均数比乙数据平均数少2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com