
| A. | $\frac{{\sqrt{3}π}}{2}$ | B. | 3π | C. | $\frac{{\sqrt{2}π}}{3}$ | D. | 2π |
分析 求出P到平面ABC的距离,AC为截面圆的直径,由勾股定理可得R2=($\frac{\sqrt{3}}{2}$)2+d2=($\frac{1}{2}$)2+($\frac{\sqrt{2}}{2}$-d)2,求出R,即可求出球的表面积.
解答 解:由题意,AC为截面圆的直径,AC=$\sqrt{3}$,
设球心到平面ABC的距离为d,球的半径为R,
∵PA=PB=1,AB=$\sqrt{2}$,∴PA⊥PB,
∵平面PAB⊥平面ABC,∴P到平面ABC的距离为$\frac{\sqrt{2}}{2}$.
由勾股定理可得R2=($\frac{\sqrt{3}}{2}$)2+d2=($\frac{1}{2}$)2+($\frac{\sqrt{2}}{2}$-d)2,
∴d=0,R2=$\frac{3}{4}$,
∴球的表面积为4πR2=3π.
故选:B
点评 本题考查球的表面积,考查学生的计算能力,求出球的半径是关键.属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
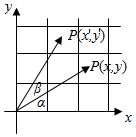 如图,设OP与x轴的正方向的夹角为α,OP'与OP的夹角为β,现将OP绕O点旋转到与OP'重合,旋转角β=$\frac{π}{6}$,则这个旋转变换对应的矩阵为$[\begin{array}{l}{\frac{\sqrt{3}}{2}}&{-\frac{1}{2}}\\{\frac{1}{2}}&{\frac{\sqrt{3}}{2}}\end{array}]$.
如图,设OP与x轴的正方向的夹角为α,OP'与OP的夹角为β,现将OP绕O点旋转到与OP'重合,旋转角β=$\frac{π}{6}$,则这个旋转变换对应的矩阵为$[\begin{array}{l}{\frac{\sqrt{3}}{2}}&{-\frac{1}{2}}\\{\frac{1}{2}}&{\frac{\sqrt{3}}{2}}\end{array}]$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com