Question

13．设函数f（x）=x²+ax+3．
（1）当x∈R时，f（x）≥a恒成立，求a的取值范围；
（2）当x∈[-2，2]时，f（x）≥a恒成立，求a的取值范囤；
（3）设不等式f（x）≥a对于满足1≤a≤3的一切a的取值都成立，求x的取值范围．

Answer 1

分析 （1）对一切实数x恒成立，转化为二次函数恒为非负，利用根的判别式小于等于0即可；
（2）对于[-2，2]区间内的任意x恒成立，同样考虑二次函数的最值问题，按区间与对称轴的关系分三种情况讨，最后结合图象即可解决问题；
（3）令g（x）=x²+ax+3-a≥0，通过a的范围得到△≤0，从而求出x的范围即可．

解答 解：（1）∵x∈R时，有x²+ax+3-a≥0恒成立，
须△=a²-4（3-a）≤0，即a²+4a-12≤0，所以-6≤a≤2．
（2）当x∈[-2，2]时，设g（x）=x²+ax+3-a≥0，
分如下三种情况讨论（如图所示）：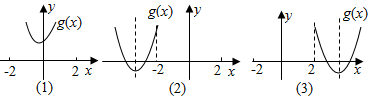

①如图（1），当g（x）的图象恒在x轴上方时，满足条件时，有△=a²-4（3-a）≤0，即-6≤a≤2．
②如图（2），g（x）的图象与x轴有交点，
当-$\frac{a}{2}$≤-2时，g（x）≥0，
即 $\left\{\begin{array}{l}{△≥0}\\{x=-\frac{a}{2}≤-2}\\{g（-2）≥0}\end{array}\right.$，即 $\left\{\begin{array}{l}{{a}^{2}-4（3-a）≥0}\\{-\frac{a}{2}≤-2}\\{4-2a+3-a≥0}\end{array}\right.$?$\left\{\begin{array}{l}{a≥2或a≤-6}\\{a≥4}\\{a≤\frac{7}{3}}\end{array}\right.$解之得a∈Φ．
③如图（3），g（x）的图象与x轴有交点，
-$\frac{a}{2}$≥-2时，g（x）≥0，即 $\left\{\begin{array}{l}{△≥0}\\{x=-\frac{a}{2}≥2}\\{g（2）≥0}\end{array}\right.$即 $\left\{\begin{array}{l}{{a}^{2}-4（3-a）≥0}\\{-\frac{a}{2}≥2}\\{4+2a+3-a≥0}\end{array}\right.$?$\left\{\begin{array}{l}{a≥2或a≤-6}\\{a≤-4}\\{a≥-7}\end{array}\right.$?-7≤a≤-6
综合①②③得a∈[-7，2]．
（3）令g（x）=x²+ax+3-a≥0，
则△=a²-4（3-a）=a²+a-12=${（a+\frac{1}{2}）}^{2}$-$\frac{49}{4}$，
∵1≤a≤3，∴$\frac{9}{4}$≤${（a+\frac{1}{2}）}^{2}$≤$\frac{49}{4}$，
∴△≤0，
∴x∈R．

点评 本题主要了一元二次不等式恒成立的问题，注意（1）、（2）两问的不同点，都是利用了二次函数图象的特点数形结合解决问题的．