
分析 设以(1,1)为中点的弦交椭圆$C:\frac{x^2}{9}+\frac{y^2}{5}=1$交于A(x1,y1),B(x2,y2),由中点从坐标公式知x1+x2=2,y1+y2=2,把A(x1,y1),B(x2,y2)分别代入5x2+9y2=45,得5x12+9y12=45…①5x22+9y22=45…②,①-②,得5(x1-x2)+9(y1-y2)=0,求得k即可.
解答 解:设以(1,1)为中点的弦交椭圆$C:\frac{x^2}{9}+\frac{y^2}{5}=1$交于A(x1,y1),B(x2,y2),
由中点从坐标公式知x1+x2=2,y1+y2=2,
把A(x1,y1),B(x2,y2)分别代入5x2+9y2=45,得
5x12+9y12=45…①5x22+9y22=45…②
①-②,得5(x1-x2)+9(y1-y2)=0,
k=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}=-\frac{5}{9}$,
∴此弦所在的直线方程为y-1=-$\frac{5}{9}$(x-1),
即5x+9y-14=0.
故答案为:5x+9y-14=0.
点评 本题考查椭圆的性质和应用,点差法的合理运用,属于基础题.


科目:高中数学 来源: 题型:解答题
| x | $-\sqrt{2}$ | 2 | $\sqrt{6}$ | 9 |
| y | $\sqrt{3}$ | $-\sqrt{2}$ | -1 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| PM2.5日均值k(微克) | 空气质量等级 |
| k≤35 | 一级 |
| 35<k<75 | 二级 |
| k>75 | 超标 |
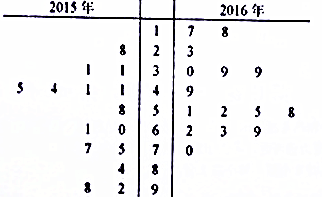
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{2}{5}$ | C. | $\frac{7}{10}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com