Question

20．已知椭圆$\frac{x^2}{25}$+$\frac{y^2}{16}$=1内有两点A（1，3），B（3，0），P为椭圆上一点，则|PA|+|PB|的最大值为（　　）

• A． 10
• B． 15
• C． 4
• D． 5

Answer 1

分析 根据椭圆的方程，算出它的焦点坐标为B（3，0）和B'（-3，0）．因此连接PB'、AB'，根据椭圆的定义得|PA|+|PB|=|PA|+（2a-|PB'|）=10+（|PA|-|PB'|）．再由三角形两边之差小于第三边，得到当且仅当点P在AB'延长线上时，|PA|+|PB|=10+|AB'|=15达到最大值，从而得到本题答案．

解答 解：∵椭圆$\frac{x^2}{25}$+$\frac{y^2}{16}$=1，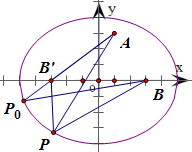
∴焦点坐标为B（3，0）和B'（-3，0）
连接PB'、AB'，根据椭圆的定义，得|PB|+|PB'|=2a=10，
可得|PB|=10-|PB'|，
因此，|PA|+|PB|=|PA|+（10-|PB'|）=10+（|PA|-|PB'|）
∵|PA|-|PB'|≤|AB'|，
∴|PA|+|PB|≤10+|AB'|=10+$\sqrt{（1+3）^{2}+（3-0）^{2}}$=10+5=15，
当且仅当点P在AB'延长线上时，等号成立．
综上所述，可得|PA|+|PB|的最大值为15．
故选B．

点评 本题给出椭圆内部一点A，求椭圆上动点P与A点和一个焦点距离B和的最大值，着重考查了椭圆的定义、标准方程和简单几何性质等知识，属于中档题．