Question

18．如图是正方体的平面展开图．关于这个正方体，有以下判断：
①ED与NF所成的角为60°
②CN∥平面AFB
③BM∥DE
④平面BDE∥平面NCF
其中正确判断的序号是（　　）

• A． ①③
• B． ②③
• C． ①②④
• D． ②③④

Answer 1

分析 在①中，由NF∥BD，知∠EDB是ED与NF所成角（或所成角的补角），由△EDB是等边三角形，得ED与NF所成的角为60°；在②中，由CN∥EB，得CN∥平面AFB；在③中，由BM∥AN，DE与AN相交，得BM与DE不平行；在④中，由NF∥BD，CF∥DE，得平面BDE∥平面NCF．

解答 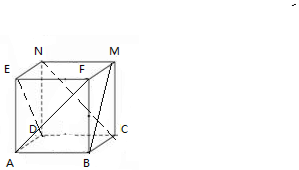解：把正方体的平面展开图还原成正方体ABCD-EFMN，
在①中，∵NF∥BD，∴∠EDB是ED与NF所成角（或所成角的补角），
∵△EDB是等边三角形，∴∠EDB=60°，
∴ED与NF所成的角为60°，故①正确；
在②中，∵CN∥EB，CN?平面AFB，EB?平面AFB，
∴CN∥平面AFB，故②正确；
在③中，∵BM∥AN，DE与AN相交，∴BM与DE不平行，故③错误；
在④中，∵NF∥BD，CF∥DE，NF∩CF=F，DE∩DB=D，
NF、FC?平面CNF，DE、DB?平面BDE，
∴平面BDE∥平面NCF，故④正确．
故选：C．

点评 本题考查命题真假的判断，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查化归与转化思想、数形结合思想，是中档题．