Question

7．若半径为2 的球O中有一内接圆柱，当圆柱的侧面积为8π时，圆柱的体积为4$\sqrt{2}π$．

Answer 1

分析 设半径为R=2 的球O中的内接圆柱的高为h，底面半径为r，由圆柱的侧面积为8π，列出方程组，求出r=$\sqrt{2}$，h=2$\sqrt{2}$，由此能求出圆柱的体积．

解答 解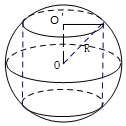：如图，设半径为R=2 的球O中的内接圆柱的高为h，底面半径为r，
∵圆柱的侧面积为8π，
∴$\left\{\begin{array}{l}{2πrh=8π}\\{{r}^{2}+（\frac{1}{2}h）^{2}=4}\end{array}\right.$，解得r=$\sqrt{2}$，h=2$\sqrt{2}$，
∴圆柱的体积V=πr²h=$π×（\sqrt{2}）^{2}×2\sqrt{2}$=4$\sqrt{2}π$．
故答案为：4$\sqrt{2}π$．

点评 本题考查圆柱的体积的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查化归与转化思想、数形结合思想，是中档题．