
分析 根据条件判断数列{an}是以2为首项,公比为2的等比数列,结合等比数列的前n项和公式进行求解即可.
解答 解:∵a1=2,a6=32,anan+2=an+12,
∴数列{an}是以2为首项,公比为2的等比数列
∴an=2n,
则第m-1组的最后一个数为${a}_{{(m-1)}^{2}}$=${2}^{(m-1)^{2}}$,
则第m组的第一个数${a}_{(m-1)^{2}+1}$=${2}^{(m-1)^{2}+1}$,
则当m≥3时,A(m,1),A(m,2),…A(m,n)构成以${a}_{(m-1)^{2}+1}$=${2}^{(m-1)^{2}+1}$为首项,公比q=2的等比数列,
则当m≥3时,A(m,1)+A(m,2)+…+A(m,n)
=${2}^{(m-1)^{2}+1}$$•\frac{1-{2}^{n}}{1-2}$=${2}^{(m-1)^{2}}$•2×(2n-1)
=${2}^{(m-1)^{2}}$•(2n+1-2).
故答案为:${2}^{(m-1)^{2}}$•(2n+1-2).
点评 本题主要考查数列的递推公式的应用,根据条件判断数列是等比数列以及利用等比数列的前n项和公式是解决本题的关键.考查学生的运算和推理能力.


科目:高中数学 来源: 题型:选择题
| A. | P(ξ=2) | B. | P(ξ=3) | C. | P(ξ≤2) | D. | P(ξ≤3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
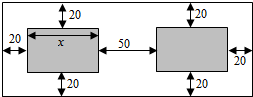 某单位因工作需要,要制作一批操作台面,台面上有两块大小相同的长方形钢化玻璃(图中阴影部分),每块钢化玻璃的面积为1800cm2,每块钢化玻璃需能放置半径为15cm的圆形器皿,每块钢化玻璃周围与操作台边缘要留20cm空白,两块钢化玻璃的间距为50cm,设钢化玻璃长为xcm,操作台面面积为S.
某单位因工作需要,要制作一批操作台面,台面上有两块大小相同的长方形钢化玻璃(图中阴影部分),每块钢化玻璃的面积为1800cm2,每块钢化玻璃需能放置半径为15cm的圆形器皿,每块钢化玻璃周围与操作台边缘要留20cm空白,两块钢化玻璃的间距为50cm,设钢化玻璃长为xcm,操作台面面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com