已知函数f(x)=|x+1|+|x-3|．＜6的解集,≥|2a+1|不恒成立.求实数a的取值范围．题目和参考答案——青夏教育精英家教网—

4．已知函数f（x）=|x+1|+|x-3|．
（1）求不等式f（x）＜6的解集；
（2）若关于x的不等式f（x）≥|2a+1|不恒成立，求实数a的取值范围．

分析（1）分类讨论，即可解不等式；
（2）求出f（x）_min=4，关于x的不等式f（x）≥|2a+1|不恒成立，可得|2a+1|＞4，即可求实数a的取值范围．

解答解：（1）x≤-1，|x+1|+|x-3|＜6可化为-x-1-x+3＜6，∴x＞-2，∴-2＜x≤-1．
-1＜x＜3，|x+1|+|x-3|＜6可化为x+1-x+3＜6，∴-2＜x≤-1；
x≥3，|x+1|+|x-3|＜6可化为x+1+x-3＜6，∴x＜4，∴-2＜x≤-1，
综上所述，不等式的解集为{x|-2＜x＜4}；
（2）∵f（x）=|x+1|+|x-3|≥|x+1-x+3|=4当且仅当-1≤x≤3时，等号成立，即f（x）_min=4．
∵关于x的不等式f（x）≥|2a+1|不恒成立，
∴|2a+1|＞4，∴a＜-2.5或a＞1.5．

点评本题考查不等式的解法，考查不恒成立问题，考查学生的计算能力，属于中档题．

练习册系列答案

黄冈海淀大考卷单元期末冲刺100分系列答案

课时掌控随堂练习系列答案

课堂新动态系列答案

一课一练一本通系列答案

初中历史与社会思想品德精讲精练系列答案

浙江之星学业水平测试系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

8．已知焦点在x轴上，离心率为$\frac{{\sqrt{6}}}{3}$的椭圆C的一个顶点是（0，1）．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）设直线l与椭圆C交于A、B两点，且OA⊥OB，O为坐标原点，判断直线l与圆x²+y²=1的位置关系？证明你的结论．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

15．复数z=（a²-1）+（a-1）i（a∈R）为纯虚数，则z=（　　）

A．

B．

-2i

C．

D．

-i

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

12．“x＜3”是“ln（x-2）＜0”的（　　）

	A．	充分不必要条件		B．	必要不充分条件
	C．	充分必要条件		D．	既不充分也不必要条件

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

19．

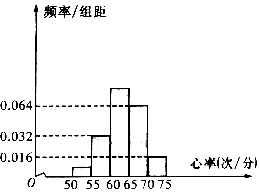某学校的特长班有50名学生，其中有体育生20人，艺术生30名，在学校组织的一次体检中，该班所有学生进行了心率测试，心率全部介于50次/分到75次/分之间，现将数据分成五组，第一组[50，55），第二组[55，60），…，第五组[70，75），按上述分组方法得到的频率分布直方图如图所示，已知图中从左到右的前三组的频率之比为a：4：10．
（1）求a的值，并求这50名学生心率的平均数；
（2）因为学习专业的原因，体育生常年进行系统的身体锻炼，艺术生则很少进行系统的身体锻炼，若从第一组和第二组的学生中随机抽取一名，该学生是体育生的概率为0.8，请将下面的列联表补充完整，并判断是否有99.5%的把握认为心率小于60次/分与常年进行系统的身体锻炼有关？请说明理由．
参考数据：

P（K²≥k₀）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k₀	2.072	2.706	3.841	5.024	6.635	7.879	10.828

参考公式：K²=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d

	心率小于60次/分	心率不小于60次/分	合计
体育生	8	12	20
艺术生	2	28	30
合计	10	40	50

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

9．已知双曲线${C_1}：\frac{x^2}{6}-\frac{y^2}{2}=1$与双曲线${C_2}：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的离心率相同，且双曲线C₂的左、右焦点分别为F₁，F₂，M是双曲线C₂一条渐近线上的某一点，且OM⊥MF₂，${S_{△OM{F_2}}}=8\sqrt{3}$，则双曲线C₂的实轴长为（　　）

A．

B．

$4\sqrt{3}$

C．

D．

$8\sqrt{3}$

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

16．上世纪八十年代初，邓小平同志曾指出“在人才的问题上，要特别强调一下，必须打破常规去发现、选拔和培养杰出的人才”．据此，经省教育厅批准，某中学领导审时度势，果断作出于1985年开始施行超常实验班教学试验的决定．一时间，学生兴奋，教师欣喜，家长欢呼，社会热议．该中学实验班一路走来，可谓风光无限，硕果累累，尤其值得一提的是，1990年，全国共招收150名少年大学生，该中学就有19名实验班学生被录取，占全国的十分之一，轰动海内外．设该中学超常实验班学生第x年被录取少年大学生的人数为y．
（1）左下表为该中学连续5年实验班学生被录取少年大学生人数，求y关于x的线性回归方程，并估计第6年该中学超常实验班学生被录取少年大学生人数；

年份序号x	1	2	3	4	5
录取人数y	10	11	14	16	19

附1：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline y$-$\stackrel{∧}{b}$$\overline{x}$
（2）如表是从该校已经毕业的100名高中生录取少年大学生人数与是否接受超常实验班教育得到2×2列联表，完成上表，并回答：是否有95%以上的把握认为“录取少年大学生人数与是否接受超常实验班教育有关系”．
附2：

	接受超常实验班教育	未接受超常实验班教育	合计
录取少年大学生	60	20	80
未录取少年大学生	10	10	20
合计	70	30	100

P（k²≥k₀）	0.50	0.40	0.10	0.05
k₀	0.455	0.708	2.706	3.841

K²=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，n=a+b+c+d．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

13．已知函数f（x）=|lnx-$\frac{a}{x}$|+b，其中a，b∈R且a＞2，若f（2）=$\frac{e}{2}$-ln2+1，f（x）在（1，f（1））处切线的斜率为-e-1．
（1）求函数f（x）的解析式及其单调区间；
（2）若实数c，d满足cd=λ，且f（c）＜f（d）对于任意c＞d恒成立，求实数λ的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

14．在△ABC中，AB=8，BC=7，AC=5，则AB边上的高是$\frac{5\sqrt{3}}{2}$．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学