练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．计算：（C${\;}_{15}^{0}$）2+（C${\;}_{15}^{1}$）2+（C${\;}_{15}^{2}$）2+…+（C${\;}_{15}^{15}$）2．

    分析 由（1+x）15•（1+x）15=（1+x）30，在展开式中比较x15系数即可求解．

    解答 解：（1+x）15•（1+x）15=（1+x）30，
    ∴$（{C}_{15}^{0}+{C}_{15}^{1}x+…+{C}_{15}^{15}{x}^{15}）$•$（{C}_{15}^{0}+{C}_{15}^{1}x+…+{C}_{15}^{15}{x}^{15}）$=$（{C}_{30}^{0}+{C}_{30}^{1}x+…+{C}_{30}^{30}{x}^{30}）$，
    比较x15系数可得，${C}_{15}^{0}{C}_{15}^{15}$$+{C}_{15}^{1}{C}_{15}^{14}+{C}_{15}^{2}{C}_{15}^{13}+…+{C}_{15}^{15}{C}_{15}^{0}$=${C}_{30}^{15}$，
    ∴（C${\;}_{15}^{0}$）2+（C${\;}_{15}^{1}$）2+（C${\;}_{15}^{2}$）2+…+（C${\;}_{15}^{15}$）2=${C}_{30}^{15}$．

    点评 本题主要考查了二项展开式的应用，解题关键是根据已知式子构造展开式中指定项的系数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    5．已知某个车轮旋转的角度α（弧度）与时间t（秒）的函数关系是α=$\frac{2π}{0.64}$t2（t≥0），则车轮启动后第1.6秒时的瞬时角速度是（　　）
    A．20π弧度/秒B．10π弧度/秒C．8π弧度/秒D．5π弧度/秒

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．设平面向量组ai （i=1，2，3，…）满足：①|ai|=1；②ai•ai+1=0，设Tn=|a1+a2+…+an|（n≥2），则T4的最大值为$2\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．用不等号（＞，＜）填空：$\frac{sin100°}{sin200°cos300°cos100°}$＞0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．用符号语言表示下列图形中几何元素之间的位置关系．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．求证：1+$\frac{1}{3^2}$+$\frac{1}{5^2}$+…+$\frac{1}{（2n-1）^2}$＞$\frac{7}{6}$-$\frac{1}{2（2n+1）}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

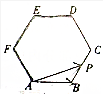    7．如图所示，点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动，其中AB=k，则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间为[$-\frac{k}{2}$，0]∪[k，$\frac{3}{2}{k}^{2}$]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．不等式${A}_{8}^{x}$＜6${A}_{8}^{x-2}$的解集为{8}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知函数f（x）=2x-2-x，若f（a）=3，求f（2a）的值．

    查看答案和解析>>

    同步练习册答案