
分析 利用二倍角的余弦函数公式及同角三角函数间的基本关系化简,再利用同角三角函数间的基本关系弦化切后,将已知等式代入病利用同角三角函数间的基本关系切化弦后,抵消得到结果.
解答 解:cos2θ=cos2θ-sin2θ=$\frac{co{s}^{2}θ-si{n}^{2}θ}{co{s}^{2}θ+si{n}^{2}θ}$=$\frac{1-ta{n}^{2}θ}{1+ta{n}^{2}θ}$=$\frac{-2ta{n}^{2}φ}{2ta{n}^{2}φ+2}$=$\frac{-ta{n}^{2}φ}{ta{n}^{2}φ+1}$=$\frac{-si{n}^{2}φ}{si{n}^{2}φ+co{s}^{2}φ}$=-sin2φ.
∴cos2θ+sin2φ=0.
故答案为:0.
点评 此题考查了二倍角的余弦函数公式,以及同角三角函数间的基本关系,熟练掌握公式是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 8 | 3 | 4 |
| 1 | 5 | 9 |
| 6 | 7 | 2 |
| A. | 9 | B. | 8 | C. | 6 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
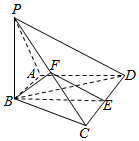 如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是棱CD和PC的中点.
如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是棱CD和PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com