Question

3．已知函数f（x）满足f（x-3）=$\frac{x}{{x}^{2}+1}$．
（1）求函数的解析式；
（2）求函数f（x）的值域．

Answer 1

分析 （1）利用换元法求出函数f（x）的解析式即可；（2）先求出函数的导数，得到函数的单调区间，从而求出函数的值域．

解答 解：（1）令z=x-3，则x=z+3，
∴f（z）=$\frac{z+3}{{（z+3）}^{2}+1}$，
∴f（x）=$\frac{x+3}{{x}^{2}+6x+10}$；
（2）f′（x）=-$\frac{（x+2）（x+4）}{{x}^{2}+6x+10}$，
令f′（x）＞0，解得：-4＜x＜-2，
令f′（x）＜0，解得：x＞-2或x＜-4，
∴f（x）在（-∞，-4），（-2，+∞）递减，在（-4，-2）递增，
又∵f（x）=$\frac{x+3}{{x}^{2}+6x+10}$=$\frac{1+\frac{3}{x}}{x+6+\frac{10}{x}}$，
当x→+∞时，f（x）→0，
当x→-∞时，f（x）→0，
∴函数f（x）的大致图象如图所示：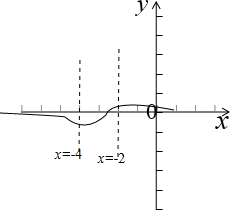
，
∴f（x）_最大值=f（x）_极大值=f（-2）=$\frac{1}{2}$，
f（x）_最小值=f（x）_极小值=f（-4）=-$\frac{1}{2}$，
∴函数f（x）的值域是：[-$\frac{1}{2}$，$\frac{1}{2}$]．

点评 本题考察了函数的解析式问题，考察函数的值域问题，本题是一道中档题．