
 如图所示,在Rt△ABC中,AC⊥BC,有AC2+BC2=AB2;类比猜想:直角四面体P-ABC(即PA⊥PB,PB⊥PC,PC⊥PA)的四个面的面积关系,证明你的猜想.
如图所示,在Rt△ABC中,AC⊥BC,有AC2+BC2=AB2;类比猜想:直角四面体P-ABC(即PA⊥PB,PB⊥PC,PC⊥PA)的四个面的面积关系,证明你的猜想. 分析 斜边的平方等于两个直角边的平方和,可类比到空间就是斜面面积的平方等于三个直角面的面积的平方和,边对应着面.即可.
解答 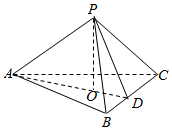 解:由边对应着面,边长对应着面积,由类比可得
解:由边对应着面,边长对应着面积,由类比可得
S2△ABC=S2△PAB+S2△PBC+S2△PCA.
证明如下:如图作PO垂直底面△ABC于O点,
连接AO并延长交BC于D,连接PD,
易证AD⊥BC,PD⊥BC,在Rt△PAD中,
由射影定理得PD2=OD•AD,
S2△PBC=($\frac{1}{2}$BC•PD)2=$\frac{1}{4}$BC2•PD2=$\frac{1}{4}$BC2•OD•AD=($\frac{1}{2}$BC•OD)($\frac{1}{2}$BC•AD)=S△ABC•S△OBC,
同理可证:S2△PBA=S△ABC•S△OBA,S2△PCA=S△ABC•S△OCA
所以:S2△PBA+S2△PCA+S2△PBC=S△ABC(•S△OBC+S△OAB+S△OAC)=S2△ABC
点评 本题考查了从平面类比到空间,属于基本类比推理.利用类比推理可以得到结论、证明类比结论时证明过程与其类比对象的证明过程类似或直接转化为类比对象的结论.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
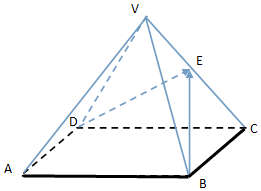 如图,在正四棱锥V-ABCD中,E为VC的中点,正四棱锥的底面边长为2a,高为h
如图,在正四棱锥V-ABCD中,E为VC的中点,正四棱锥的底面边长为2a,高为h查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈(-∞,0),x03+x0<0 | B. | ?x∈(-∞,0),x3+x≥0 | ||
| C. | ?x0∈[0,+∞),x3+x<0 | D. | ?x0∈[0,+∞),x03+x0≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一枚6点,第二枚2点 | B. | 第一枚5点,第二枚1点 | ||
| C. | 第一枚1点,第二枚6点 | D. | 第一枚6点,第二枚1点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com