
已知函数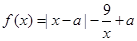 ,
,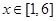 ,
,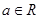 .
.
(1)若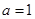 ,试判断并证明函数
,试判断并证明函数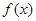 的单调性;
的单调性;
(2)当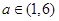 时,求函数
时,求函数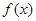 的最大值的表达式
的最大值的表达式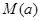 .
.
(1)判断:若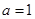 ,函数
,函数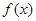 在
在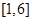 上是增函数. 用单调性的定义证明即可, (2)
上是增函数. 用单调性的定义证明即可, (2) 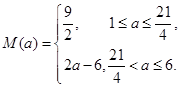
解析试题分析:(1)判断:若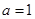 ,函数
,函数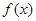 在
在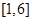 上是增函数. …………2分
上是增函数. …………2分
证明:当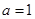 时,
时,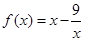 ,在区间
,在区间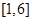 上任意
上任意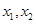 ,设
,设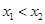 ,
,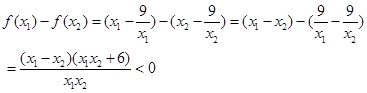
所以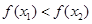 ,即
,即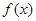 在
在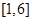 上是增函数. …… 7分
上是增函数. …… 7分
(注:用导数法证明或其它方法说明也同样给7分)
(2)因为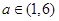 ,所以
,所以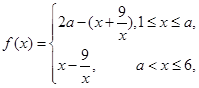 …… 9分
…… 9分
①当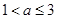 时,
时,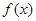 在
在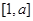 上是增函数,在
上是增函数,在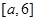 上也是增函数,
上也是增函数,
所以当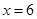 时,
时,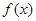 取得最大值为
取得最大值为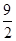 ; …… 10分
; …… 10分
②当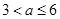 时,
时,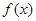 在
在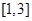 上是增函数,
上是增函数,
在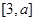 上是减函数,在
上是减函数,在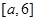 上是增函数,
上是增函数,
而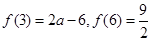 ,
,
当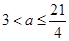 时,
时,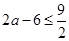 ,当
,当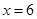 时,函数
时,函数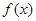 取最大值为
取最大值为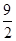 ;
;
当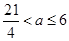 时,
时,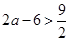 ,当
,当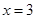 时,函数
时,函数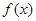 取最大值为
取最大值为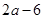 ;
;
综上得,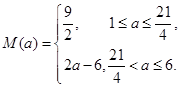 ……14分
……14分
考点:本题考查了函数的性质
点评:利用函数的单调性是解决函数最值及值域的最基本的方法,另外函数单调性的定义是证明单调性的最基本的方法,要掌握其步骤


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
已知函数 (
(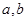
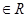 )
)
(1)若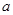 从集合
从集合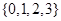 中任取一个元素,
中任取一个元素,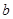 从集合
从集合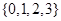 中任取一个元素,求方程
中任取一个元素,求方程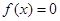 恰有两个不相等实根的概率;
恰有两个不相等实根的概率;
(2)若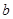 从区间
从区间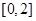 中任取一个数,
中任取一个数,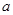 从区间
从区间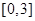 中任取一个数,求方程
中任取一个数,求方程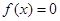 没有实根的概率.
没有实根的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com