
分析 (1)化简可知{$\frac{{S}_{n}}{n}$}是以1为首项,$\frac{3}{2}$为公差的等差数列,从而求得Sn=$\frac{1}{2}$n(3n-1),从而求{an}的通项公式;
(2)由(1)知an+1+$\frac{16}{{a}_{n}}$=3n+1+$\frac{16}{3n-2}$=3n-2+$\frac{16}{3n-2}$+3,从而利用基本不等式求最值,化恒成立问题为最值问题即可.
解答 解:(1)∵{$\frac{{S}_{n}}{n}$}是等差数列,且$\frac{{S}_{2}}{2}$+$\frac{{S}_{3}}{3}$+$\frac{{S}_{4}}{4}$=12,
∴3$\frac{{S}_{3}}{3}$=12,
∴$\frac{{S}_{3}}{3}$=4,
又∵$\frac{{S}_{1}}{1}$=1,
∴{$\frac{{S}_{n}}{n}$}是以1为首项,$\frac{3}{2}$为公差的等差数列,
故$\frac{{S}_{n}}{n}$=1+$\frac{3}{2}$(n-1)=$\frac{3n-1}{2}$,
故Sn=$\frac{1}{2}$n(3n-1),
故数列{an}是以1为首项,3为公差的等差数列,
故an=1+3(n-1)=3n-2;
(2)由(1)知,
an+1+$\frac{16}{{a}_{n}}$=3n+1+$\frac{16}{3n-2}$=3n-2+$\frac{16}{3n-2}$+3
≥2$\sqrt{16}$+3=11,
(当且仅当3n-2=$\frac{16}{3n-2}$,即n=2时,等号成立);
故若对任意的n∈N*,an+1+$\frac{16}{{a}_{n}}$≥λ恒成立,
则11≥λ,
即λ≤11.
点评 本题考查了数列的性质的判断与应用,同时考查了基本不等式的应用及恒成立问题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
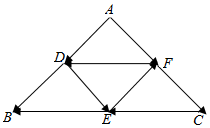 如图,D,E,F分别是等腰直角三角形ABC各边的中点,∠BAC=90°.
如图,D,E,F分别是等腰直角三角形ABC各边的中点,∠BAC=90°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com