
设函数 .
.
(Ⅰ)若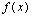 在x=
在x=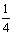 处的切线与直线4x+y=0平行,求a的值;
处的切线与直线4x+y=0平行,求a的值;
(Ⅱ)讨论函数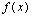 的单调区间;
的单调区间;
(Ⅲ)若函数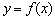 的图象与x轴交于A,B两点,线段AB中点的横坐标为
的图象与x轴交于A,B两点,线段AB中点的横坐标为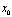 ,证明
,证明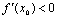 .
.
解析:(I)由题知f(x)=2ax2+(a+4)x+lnx的定义域为(0,+∞),
且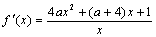 .
.
又∵f(x)的图象在x=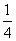 处的切线与直线4x+y=0平行,
处的切线与直线4x+y=0平行,
∴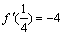 ,
,
解得a=-6.
(Ⅱ)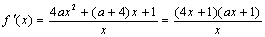 ,
,
由x>0,知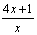 >0.
>0.
①当a≥0时,对任意x>0,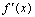 >0,
>0,
∴此时函数f(x)的单调递增区间为(0,+∞).
②当a<0时,令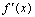 =0,解得
=0,解得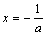 ,
,
当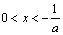 时,
时,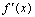 >0,当
>0,当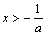 时,
时,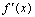 <0,
<0,
此时,函数f(x)的单调递增区间为(0,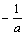 ),单调递减区间为(
),单调递减区间为(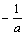 ,+∞).
,+∞).
(Ⅲ)不妨设A(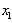 ,0),B(
,0),B(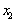 ,0),且
,0),且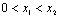 ,由(Ⅱ)知
,由(Ⅱ)知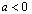 ,
,
于是要证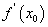 <0成立,只需证:
<0成立,只需证: 即
即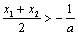 .
.
∵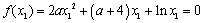 , ①
, ①
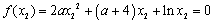 , ②
, ②
①-②得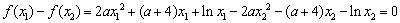 ,
,
即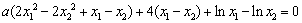 ,
,
∴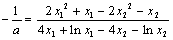 ,
,
故只需证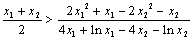 ,
,
即证明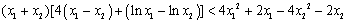 ,
,
即证明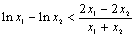 ,变形为
,变形为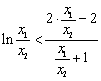 ,
,
设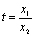
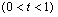 ,令
,令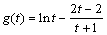 ,
,
则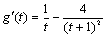
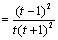 ,
,
显然当t>0时,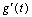 ≥0,当且仅当t=1时,
≥0,当且仅当t=1时,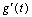 =0,
=0,
∴g(t)在(0,+∞)上是增函数.
又∵g(1)=0,
∴当t∈(0,1)时,g(t)<0总成立,命题得证.


科目:高中数学 来源: 题型:
设F1,F2分别为双曲线C: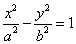 (a>0,b>0)的左、右焦点,A为双曲线的左顶点,以F1F2为直径的圆交双曲线某条渐近线于M、N两点,且满足
(a>0,b>0)的左、右焦点,A为双曲线的左顶点,以F1F2为直径的圆交双曲线某条渐近线于M、N两点,且满足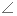 MAN=120o,则该双曲线的离心率为 ( )
MAN=120o,则该双曲线的离心率为 ( )
A. 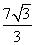 B.
B. 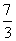 C.
C. 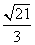 D.
D.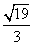
查看答案和解析>>
科目:高中数学 来源: 题型:
设某中学高三的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为y=0.85x﹣85.71,则下列结论中不正确的是( )
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心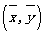
C. 若该中学高三某女生身高增加1cm,则其体重约增加0.85kg
D. 若该中学高三某女生身高为170cm,则可断定其体重必为58.79kg
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com