
分析 (I)利用余弦定理、三角函数求值、三角形内角和定理即可得出.
(II)利用等差数列与等比数列的通项公式可得an,再利用“裂项求和”方法即可得出.
解答 解:(Ⅰ)由${a^2}-{(b-c)^2}=(2-\sqrt{3})bc$,得${a^2}-{b^2}-{c^2}=-\sqrt{3}bc$,
∴$cosA=\frac{{{b^2}+{c^2}-{a^2}}}{2bc}=\frac{{\sqrt{3}}}{2}$,A∈(0,π),
∴$A=\frac{π}{6}$,由$C=\frac{2π}{3}$,得$B=\frac{π}{6}$.
(Ⅱ)设{an}的公差为d,由(I)得${a_1}=\frac{1}{{cos\frac{π}{3}}}=2$,且${a_4}^2={a_2}{a_8}$,
∴${({a_1}+3d)^2}=({a_1}+d)({a_1}+7d)$,又d≠0,∴d=2,
∴an=2n,
∴$\frac{4}{{{a_n}{a_{n+1}}}}$=$\frac{1}{n}-\frac{1}{n+1}$,
∴${S_n}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+…+\frac{1}{n}-\frac{1}{n+1}=\frac{n}{n+1}$.
点评 本题考查了余弦定理、三角函数求值、三角形内角和定理、等差数列与等比数列的通项公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>0} | B. | {x|-1<x<1} | C. | {x|x>1} | D. | {x|x>0或x<-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
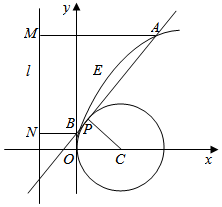 在“2016”的logo设计中,有这样一个图案
在“2016”的logo设计中,有这样一个图案 ,其由线段l、抛物线弧E及圆C三部分组成,对其进行代数化的分析,如图建系,发现:圆C方程为(x-4)2+y2=16,抛物线弧E:y2=2px(y≥0,0≤x≤8),若圆心C恰为抛物线y2=2px的焦点,线段l所在的直线恰为抛物线y2=2px的准线.
,其由线段l、抛物线弧E及圆C三部分组成,对其进行代数化的分析,如图建系,发现:圆C方程为(x-4)2+y2=16,抛物线弧E:y2=2px(y≥0,0≤x≤8),若圆心C恰为抛物线y2=2px的焦点,线段l所在的直线恰为抛物线y2=2px的准线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com