
| a1 |
| i |
| j |
| k |
| a2 |
| j |
| j |
| k |
| a3 |
| i |
| j |
| k |
| a4 |
| i |
| j |
| k |
| i |
| j |
| k |
| a4 |
| a1 |
| a2 |
| a3 |
| a4 |
| a1 |
| a2 |
| a3 |
| a4 |
| a1 |
| a2 |
| a3 |
| i |
| j |
| k |
| i |
| j |
| k |
| i |
| j |
| k |
| i |
| j |
| k |
| i |
| j |
| k |
|
| a4 |
| a1 |
| a2 |
| a3 |


科目:高中数学 来源: 题型:
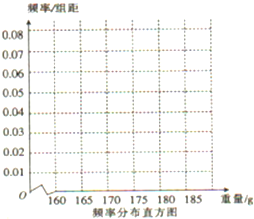 云浮市质监部门为迎接2015年春节到来,从市场中随机抽取100个不同生产厂家的某种产品检验质量,按重量(单位;g)分组(重量大的质量高),得到的频率分布表如图所示:
云浮市质监部门为迎接2015年春节到来,从市场中随机抽取100个不同生产厂家的某种产品检验质量,按重量(单位;g)分组(重量大的质量高),得到的频率分布表如图所示:| 组号 | 重量分组 | 频数 | 频率 |
| 第1组 | [160,165) | 5 | 0.050 |
| 第2组 | [165,170) | ① | 0.350 |
| 第3组 | [170,175) | 30 | ② |
| 第4组 | [175,180) | 20 | 0.200 |
| 第5组 | [180,185] | 10 | 0.100 |
| 合计 | 100 | 1.00 | |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 |
| 3 |
| 5 |
| 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| Sn |
| n |
| 1 |
| 2 |
| 4 |
| 15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com