考点:直线与平面所成的角,直线与平面垂直的性质,平面与平面垂直的判定
专题:计算题,证明题,空间位置关系与距离,空间角
分析:(1)运用线面垂直的判定和性质,即可得证;
(2)取AB的中点G,连接FG,A
1G,运用三角函数的知识,证得AE⊥A
1G,再由线面垂直的判定和面面垂直的判定定理,即可得证;
(3)以点D为坐标原点,分别以DA,DC,DD
1所在的直线为x轴,y轴,z轴建立空间直角坐标系.设正方形的边长为2,则A(2,0,0),E(2,2,1),D
1(0,0,2),F(0,1,0),求出所求向量的坐标,再设平面D
1EF的法向量为
=(x,y,z),由向量的数量积为0,求得一个法向量,再由向量的夹角公式,即可得到.
解答:
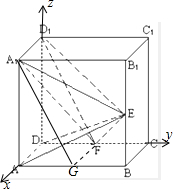
(1)证明:由于AD⊥DD
1,AD⊥CD,
则AD⊥平面CDD
1C
1,D
1F?平面CDD
1C
1,
则AD⊥D
1F;
(2)证明:取AB的中点G,连接FG,A
1G,
易得D
1FGA
1为平行四边形,则D
1F∥A
1G,
在正方形ABB
1A
1中,tan∠A
1GA=
=2,tan
∠EAB=,
即有∠A
1GA+∠EAB=90°,即有AE⊥A
1G,
即有AE⊥D
1F,又AD⊥D
1F,
则D
1F⊥平面AED,D
1F?平面A
1D
1F,
则面AED⊥面A
1FD
1;
(3)以点D为坐标原点,分别以DA,DC,DD
1所在的直线
为x轴,y轴,z轴建立空间直角坐标系.
设正方形的边长为2,则A(2,0,0),E(2,2,1),D
1(0,0,2),F(0,1,0),
=(0,2,1),
=(-2,-1,-1),
=(0,1,-2),
设平面D
1EF的法向量为
=(x,y,z),
则由
⊥可得,
•=0,即-2x-y-z=0,
⊥,可得,
•=0,即有y-2z=0,
则取
=(-3,4,2),
cos<
,
>=
=
,
设AE与平面D
1EF所成的角为θ,
则sinθ=
,cosθ=
.
则AE与平面D
1EF所成的角的余弦值为
.
点评:本题考查空间直线与平面垂直的判定和性质,以及面面垂直的判定定理和运用,考查空间的直线和平面所成的角的求法:运用法向量求解,考查运算能力,属于中档题.

 如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点. (1)证明:由于AD⊥DD1,AD⊥CD,
(1)证明:由于AD⊥DD1,AD⊥CD,

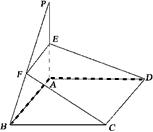 如图,点P为矩形ABCD所在平面外一点,且PA⊥平面ABCD.
如图,点P为矩形ABCD所在平面外一点,且PA⊥平面ABCD.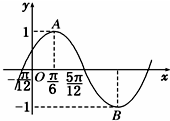 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<