
分析 (Ⅰ)向量的数量积公式计算出$\overrightarrow{e_1}$•$\overrightarrow{e_2}$=$\frac{1}{2}$,再根据数量积公式计算即可,
(Ⅱ)根据向量的和差计算,再根据向量的模即可求出答案,
(Ⅲ)根据向量的数量积为0,则夹角为90°
解答 解:∵$\overrightarrow{e_1}$、$\overrightarrow{e_2}$是夹角为60°的两个单位向量,
∴$\overrightarrow{e_1}$•$\overrightarrow{e_2}$=1×1×cos60°=$\frac{1}{2}$,
(Ⅰ)∵$\overrightarrow a=3\overrightarrow{e_1}-2\overrightarrow{e_2}$,$\overrightarrow b=2\overrightarrow{e_1}-3\overrightarrow{e_2}$,
∴$\overrightarrow a•\overrightarrow b$=6${\overrightarrow{{e}_{1}}}^{2}$+6${\overrightarrow{{e}_{2}}}^{2}$-13$\overrightarrow{e_1}$•$\overrightarrow{e_2}$=6+6-$\frac{13}{2}$=$\frac{11}{2}$;
(Ⅱ)∵$\overrightarrow a=3\overrightarrow{e_1}-2\overrightarrow{e_2}$,$\overrightarrow b=2\overrightarrow{e_1}-3\overrightarrow{e_2}$,
∴$\overrightarrow a+\overrightarrow b$=5$\overrightarrow{{e}_{1}}$-5$\overrightarrow{{e}_{2}}$,$\overrightarrow{a}$-$\overrightarrow{b}$=$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$
|$\overrightarrow a+\overrightarrow b$|2=25${\overrightarrow{{e}_{1}}}^{2}$+25${\overrightarrow{{e}_{2}}}^{2}$-50$\overrightarrow{e_1}$•$\overrightarrow{e_2}$=25+25-25=25,
|$\overrightarrow a-\overrightarrow b$|2=${\overrightarrow{{e}_{1}}}^{2}$+${\overrightarrow{{e}_{2}}}^{2}$-2$\overrightarrow{e_1}$•$\overrightarrow{e_2}$=1+1-1=1
∴|$\overrightarrow a+\overrightarrow b$|=5,|$\overrightarrow a-\overrightarrow b$|=1
(Ⅲ)($\overrightarrow a+\overrightarrow b$)($\overrightarrow a-\overrightarrow b$)=5($\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$)•($\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)=0,
∴$\overrightarrow a+\overrightarrow b$⊥$\overrightarrow a-\overrightarrow b$,
∴$\overrightarrow a+\overrightarrow b$与$\overrightarrow a-\overrightarrow b$的夹角为90°.
点评 本题考查了向量的数量积公式和向量的夹角公式以及向量的模,属于基础题.


科目:高中数学 来源: 题型:选择题
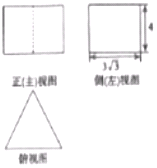 几何体三视图如图,其中俯视图为正三角形,正(主)视图与侧(左)视图为矩形,则这个几何体的体积为( )
几何体三视图如图,其中俯视图为正三角形,正(主)视图与侧(左)视图为矩形,则这个几何体的体积为( )| A. | 12$\sqrt{3}$ | B. | 36$\sqrt{3}$ | C. | 27$\sqrt{3}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16}{25}$ | B. | $\frac{16}{5}$ | C. | $\frac{32}{5}$ | D. | $\frac{25}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(2,+∞) | B. | (-2,1) | C. | (-1,2) | D. | (一∞,-2)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{9\sqrt{3}}}{4}$ | B. | $\frac{{9\sqrt{3}}}{4}$或$\frac{{3\sqrt{3}}}{4}$ | C. | $\frac{{27\sqrt{3}}}{4}$ | D. | $\frac{{27\sqrt{3}}}{4}$或$\frac{{\sqrt{3}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com