
分析 由题意可得:an=a1+(n-1)d,$\sqrt{{S}_{n}}$=$\sqrt{{a}_{1}}$+$\frac{d}{8}(n-1)$.分别令n=2,3,可得$\sqrt{2{a}_{1}+d}$=$\sqrt{{a}_{1}}$+$\frac{d}{8}$,$\sqrt{3{a}_{1}+3d}$=$\sqrt{{a}_{1}}$+$\frac{d}{4}$,联立解出即可.
解答 解:∵{an}和{$\sqrt{{S}_{n}}$}都是等差数列,{an}的公差为d,数列{$\sqrt{{S}_{n}}$}的公差为$\frac{d}{8}$,
∴an=a1+(n-1)d,$\sqrt{{S}_{n}}$=$\sqrt{{a}_{1}}$+$\frac{d}{8}(n-1)$.
分别令n=2,3,可得$\sqrt{2{a}_{1}+d}$=$\sqrt{{a}_{1}}$+$\frac{d}{8}$,$\sqrt{3{a}_{1}+3d}$=$\sqrt{{a}_{1}}$+$\frac{d}{4}$,
联立解得a1=16,d=32.
∴a1+d=48.
故答案为:48.
点评 本题考查了递推式的应用、等差数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:选择题
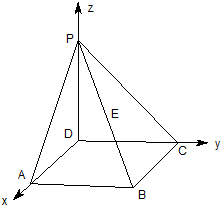 PD垂直于正方形ABCD所在平面,AB=2,E为PB的中点,cos<$\overrightarrow{DP}$,$\overrightarrow{AE}$>=$\frac{\sqrt{3}}{3}$,若以如图所示建立空间直角坐标系,则E点坐标为( )
PD垂直于正方形ABCD所在平面,AB=2,E为PB的中点,cos<$\overrightarrow{DP}$,$\overrightarrow{AE}$>=$\frac{\sqrt{3}}{3}$,若以如图所示建立空间直角坐标系,则E点坐标为( )| A. | (1,1,2) | B. | (2,2,1) | C. | (1,1,1) | D. | $(1\;,\;1\;,\;\frac{1}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | 60°或120° | C. | 30° | D. | 30°或150° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
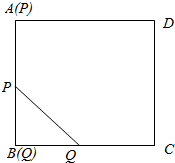 如图,正方形ABCD的边长为1,点P从顶点A沿着A→B的方向向顶点B运动,速度为2,同时,点Q从顶点B沿着B→C方向向顶点C运动,速度为1,则|PQ|的最小值为( )
如图,正方形ABCD的边长为1,点P从顶点A沿着A→B的方向向顶点B运动,速度为2,同时,点Q从顶点B沿着B→C方向向顶点C运动,速度为1,则|PQ|的最小值为( )| A. | 0 | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com