
已知f(x)=ex-ax-1.
(1)求f(x)的单调增区间;
(2)若f(x)在定义域R内单调递增,求a的取值范围.
科目:高中数学 来源: 题型:解答题
学校或班级举行活动,通常需要张贴海报进行宣传。现让你设计一张如图所示的竖向张贴的海报,要求版心面积为128dm2 ,上、下两边各空2dm,左、右两边各空1dm。如何设计海报的尺寸才能
使四周空白面积最小?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知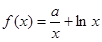 ,
, 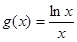 ,
,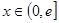 ,其中e是无理数且e="2.71828" ,
,其中e是无理数且e="2.71828" ,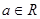 .
.
(1)若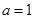 ,求
,求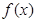 的单调区间与极值;
的单调区间与极值;
(2)求证:在(1)的条件下,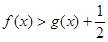 ;
;
(3)是否存在实数a,使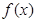 的最小值是
的最小值是 ?若存在,求出a的值;若不存在,说明理由.
?若存在,求出a的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com