
| A. | (-∞,3+$\sqrt{2}}$] | B. | (-∞,3+2$\sqrt{2}}$] | C. | (-∞,3+4$\sqrt{2}}$] | D. | (-∞,3+3$\sqrt{2}}$] |
分析 利用基本不等式可求出a+b的最小值(a+b)min,要使a+b-c≥0对于满足条件的a,b恒成立,只要值(a+b)min-c≥0即可.
解答 解:a,b都是正实数,且a,b满足$\frac{1}{a}$+$\frac{2}{b}$=1①,
则a+b=(a+b)($\frac{1}{a}$+$\frac{2}{b}$)=(3+$\frac{b}{a}$+$\frac{2a}{b}$)≥(3+2$\sqrt{\frac{b}{a}•\frac{2a}{b}}$)=3+2$\sqrt{2}$,
当且仅当$\frac{b}{a}$=$\frac{2a}{b}$即b=$\sqrt{2}$a②时,等号成立.
联立①②解得a=$\sqrt{2}$+1,b=2+$\sqrt{2}$,故a+b的最小值为3+2$\sqrt{2}$,
要使a+b-c≥0恒成立,只要3+2$\sqrt{2}$-c≥0,即c≤3+2$\sqrt{2}$,
故c的取值范围为(-∞,3+2$\sqrt{2}$].
故选:B.
点评 本题主要考查基本不等式的应用,注意基本不等式的使用条件:一正、二定、三相等,以及函数的恒成立问题.


科目:高中数学 来源: 题型:解答题
| 有影响 | 无影响 | 合计 | |
| 大一 | |||
| 大二 | |||
| 合计 |
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.789 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
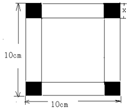 边长为10cm的正方形铁片,铁片的四角截去四个边长均为x的小正方形,然后做成一个无盖方盒.
边长为10cm的正方形铁片,铁片的四角截去四个边长均为x的小正方形,然后做成一个无盖方盒.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com