
分析 根据题意知$\frac{π}{2}$-θn是直线OAn的倾斜角,化$\frac{co{sθ}_{n}}{si{nθ}_{n}}$=$\frac{sin(\frac{π}{2}{-θ}_{n})}{cos(\frac{π}{2}{-θ}_{n})}$=tan($\frac{π}{2}$-θn)=$\frac{f(n)}{n}$,再求出$\frac{cos{θ}_{1}}{sin{θ}_{1}}$+$\frac{cos{θ}_{2}}{sin{θ}_{2}}$+$\frac{cos{θ}_{3}}{sin{θ}_{3}}$+…+$\frac{cos{θ}_{n}}{sin{θ}_{n}}$的解析式g(n),利用g(n)<t恒成立求出t的最小值.
解答 解:根据题意得,$\frac{π}{2}$-θn是直线OAn的倾斜角,
∴$\frac{co{sθ}_{n}}{si{nθ}_{n}}$=$\frac{sin(\frac{π}{2}{-θ}_{n})}{cos(\frac{π}{2}{-θ}_{n})}$
=tan($\frac{π}{2}$-θn)
=$\frac{f(n)}{n}$
=$\frac{2}{n(n+2)}$
=$\frac{1}{n}$-$\frac{1}{n+2}$,
∴$\frac{cos{θ}_{1}}{sin{θ}_{1}}$+$\frac{cos{θ}_{2}}{sin{θ}_{2}}$+$\frac{cos{θ}_{3}}{sin{θ}_{3}}$+…+$\frac{cos{θ}_{n}}{sin{θ}_{n}}$
=(1-$\frac{1}{3}$)+($\frac{1}{2}$-$\frac{1}{4}$)+($\frac{1}{3}$-$\frac{1}{5}$)+…+($\frac{1}{n}$-$\frac{1}{n+2}$)
=1+$\frac{1}{2}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$
=$\frac{3}{2}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$;
要使$\frac{3}{2}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$<t恒成立,
只须使实数t的最小值为$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题考查了平面向量的应用问题,也考查了直线的倾斜角与斜率以及不等式恒成立问题,是综合题.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:填空题
| x | 1 | 2 | 3 | 4 | 5 |
| y | 13.2 | m | 14.2 | 15.4 | 16.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4032 | B. | 2016 | C. | 4034 | D. | 2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
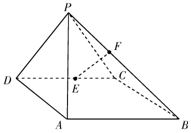 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,$AB=DP=2\sqrt{2}$,E为CD的中点,点F在线段PB上.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,$AB=DP=2\sqrt{2}$,E为CD的中点,点F在线段PB上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com