
如图,正方体ABCD-A1B1C1D1中,E,F分别在A1D,AC上,且A1E=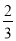 A1D,AF=
A1D,AF= AC,则( )
AC,则( )
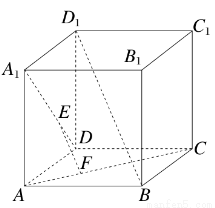
A.EF至多与A1D,AC之一垂直
B.EF⊥A1D,EF⊥AC
C.EF与BD1相交
D.EF与BD1异面
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-3圆的方程(解析版) 题型:解答题
已知圆C经过点A(-2,0),B(0,2),且圆心C在直线y=x上,又直线l:y=kx+1与圆C相交于P、Q两点.
(1)求圆C的方程;
(2)过点(0,1)作直线l1与l垂直,且直线l1与圆C交于M、N两点,求四边形PMQN面积的最大值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-1直线的倾斜角与斜率、直线方程(解析版) 题型:填空题
已知点A(3,0),B(0,4),直线AB上一动点P(x,y),则xy的最大值是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-7立体几何中的向量方法(解析版) 题型:选择题
如图所示,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF.当A1、E、F、C1共面时,平面A1DE与平面C1DF所成二面角的余弦值为( )
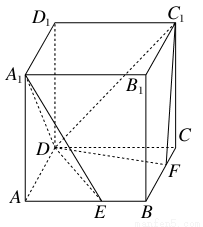
A.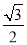 B.
B.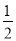 C.
C.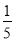 D.
D.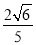
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-6空间向量及运算(解析版) 题型:解答题
如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E、F、G分别是AB、AD、CD的中点,计算:
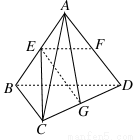
(1) ·
·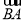 ;
;
(2) ·
·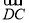 ;
;
(3)EG的长;
(4)异面直线AG与CE所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-6空间向量及运算(解析版) 题型:选择题
已知向量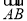 =(2,4,5),
=(2,4,5), =(3,x,y),若
=(3,x,y),若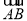 ∥
∥ ,则( )
,则( )
A.x=6,y=15 B.x=3,y=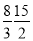
C.x=3,y=15 D.x=6,y=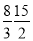
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-5直线、平面垂直的判定及性质(解析版) 题型:填空题
设α、β、γ为彼此不重合的三个平面,l为直线,给出下列命题:
①若α∥β,α⊥γ,则β⊥γ;
②若α⊥γ,β⊥γ,且α∩β=l,则l⊥γ;
③若直线l与平面α内的无数条直线垂直,则直线l与平面α垂直;
④若α内存在不共线的三点到β的距离相等,则平面α平行于平面β;
上面命题中,真命题的序号为________(写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-4直线、平面平行的判定及性质(解析版) 题型:选择题
如图中四个正方体图形,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是( )
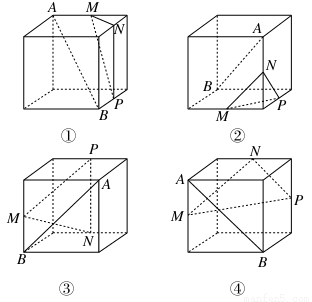
A.①③ B.①④ C.②③ D.②④
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-7数学归纳法(解析版) 题型:填空题
若f(n)=12+22+32+…+(2n)2,则f(k+1)与f(k)的递推关系式是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com