练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在中，，，为线段的垂直平分线，与交与点为上异于的任意一点.

    求的值；

    判断的值是否为一个常数，并说明理由．

    【答案】14；是.

    【解析】

    法一：由题意及图形，可把向量用两个向量的表示出来，再利用数量积的公式求出数量积；

    将向量用与表示出来，再由向量的数量积公式求数量积，根据其值的情况确定是否是一个常数；

    法二：由题意可以以BC所在直线为x轴，DE所在直线为y轴建立坐标系，得出各点的坐标，由向量坐标的定义式求出的坐标表示，由向量的数量积公式求数量积；

    设E点坐标为，表示出向量的坐标再由向量的数量积坐标表示公式求数量积即可.

    法1：由已知可得，，

    ,

    的值为一个常数为线段BC的垂直平分线，L与BC交与点D，E为L上异于D的任意一点，

    ，

    故：

    解法2：以D点为原点，BC所在直线为x轴，L所在直线为 y轴建立直角坐标系，可求，

    此时，，

    设E点坐标为，

    ，

    常数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】建造一间地面面积为12的背面靠墙的猪圈, 底面为长方形的猪圈正面的造价为120元/, 侧面的造价为80元/, 屋顶造价为1120元. 如果墙高3, 且不计猪圈背面的费用, 问怎样设计能使猪圈的总造价最低, 最低总造价是多少元?

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，己知△BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，∠ADB=60°，E、F分别是AC、AD上的动点，且 =λ（0＜λ＜1）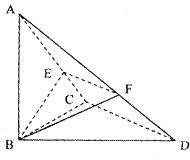
    （1）求证：不论λ为何值，总有EF⊥平面ABC：
    （2）若λ= ，求三棱锥A﹣BEF的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着移动互联网的快速发展，基于互联网的共享单车应运而生.某共享单车运营公司为进一步扩大市场，公司拟再采购一批单车.现有采购成本分别为元/辆和元/辆的、两款车型可供选择，按规定每辆单车最多使用年，但由于多种原因（如骑行频率等）会导致车辆报废年限各不相同.考虑到公司运营的经济效益，该公司决定先对两款车型的单车各辆进行科学模拟测试，得到两款单车使用寿命频数表见下表.

    经测算，平均每辆单车每年可以带来收入元.不考虑除采购成本之外的其他成本，假设每辆单车的使用寿命都是整年.

    （1）分别估计、两款车型使用寿命不低于年的概率；

    （2）如果你是公司的负责人，以参加科学模拟测试的两款车型各辆单车产生利润的平均数为决策依据，你会选择采购哪款车型？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ，则f（f（﹣2））= ， 若f（x）≥2，则x的取值范围为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点，是函数（，）图象上的任意两点，且角的终边经过点，若时，的最小值为．

    （1）求函数的解析式；

    （2）当时，不等式恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在直角坐标系中，曲线的方程是，直线经过点，倾斜角为，以为极点，轴的正半轴为极轴建立极坐标系.

    （1）写出曲线的极坐标方程和直线的参数方程；

    （2）设直线与曲线相交于，两点，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(2016～2017·郑州高一检测)过点M(1,2)的直线l与圆C：(x－3)2＋(y－4)2＝25交于A，B两点，C为圆心，当∠ACB最小时，直线l的方程是 (　　)

    A. x－2y＋3＝0 B. 2x＋y－4＝0

    C. x－y＋1＝0 D. x＋y－3＝0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面，，，，为上一点，且.

    （1）求证：平面；

    （2）若，，，求三棱锥的体积.

    查看答案和解析>>

    同步练习册答案