练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．利用杨辉三角解不等式${C}_{m}^{4}$＞${C}_{m}^{7}$，不等式的解集为{7，8，9，10}．

    分析 画出杨辉三角的部分，得到数字呈现出的规律，即自左向右先增后减，且对称呈现，由此得到不等式${C}_{m}^{4}$＞${C}_{m}^{7}$的解集．

    解答 解：杨辉三角如图，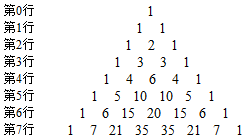

    由题意知，m≥7，当m=7时，不等式成立，
    当m=8，9，10时，不等式${C}_{m}^{4}$＞${C}_{m}^{7}$成立，
    当m=11时，有${C}_{11}^{4}={C}_{11}^{7}$，当m≥12时，${C}_{m}^{4}$离左端点数值近，而${C}_{m}^{7}$离右端点数值远，${C}_{m}^{4}＜{C}_{m}^{7}$．
    ∴不等式${C}_{m}^{4}$＞${C}_{m}^{7}$的解集为{7，8，9，10}．
    故答案为：{7，8，9，10}．

    点评 本题考查不等式的解法，训练了杨辉三角在求解不等式中的应用，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    20．已知$\overrightarrow{a}$=（1-cosθ，1），$\overrightarrow{b}$=（1+cosθ，-sinθ），θ∈R，则$\overrightarrow{a}$$•\overrightarrow{b}$的最小值为$-\frac{1}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．函数f（x）=$\frac{cosx•ln（1+x）}{x}$的部分图象大致为（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．求值：cos（x+27°）cos（x-18°）+sin（x+27°）sin（x-18°）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知角α终边上一点P（-4，3），求$\frac{sin（\frac{π}{2}-α）cos（2π-α）tan（-α+3π）}{tan（π+α）sin（\frac{π}{2}+α）}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知函数f（x）=loga（x-2）+4（a＞0且a≠1），其图象过定点P，角α的始边与x轴的正半轴重合，顶点与坐标原点重合，终边过点P，则$\frac{sinα+2cosα}{sinα-cosα}$=10．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．求函数y=sin2x+2cosxsinx-cos2x的最大值、最小值和周期．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=l（a＞0，b＞0）的一条渐近线与直线2x+y-3=0垂直，则该双曲线的离心率为$\frac{\sqrt{5}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．某集团计划调整某种产品的价格，为此销售部在3月1日至3月5日连续五天对某个大型批发市场中该产品一天的销售量及其价格进行了调查，其中该产品的价格x（元）与销售量y（万件）之间的数据如表所示：
    日期3月1日3月2日3月3日3月4日3月5日
    价格x（元）99.51010.511
    销售量y（万件）1110865
    已知销售量y与价格x之间具有线性相关关系，其回归直线方程为：y=bx+40，若该集团调整该产品的价格到10.2元，预测批发市场中该产品的日销售量约为（　　）
    A．7.66万件B．7.86万件C．8.06万件D．7.36万件

    查看答案和解析>>

    同步练习册答案