
分析 (Ⅰ)求出函数f(x)的导函数,得到导函数的零点,由导函数的零点对定义域分段,列表后可得f(x)的单调区间;
(Ⅱ)(i)求出g(x)的导函数,由题意知$\left\{\begin{array}{l}g({x_0})={e^{x_0}}\\ g'({x_0})={e^{x_0}}\end{array}\right.$,求解可得$\left\{\begin{array}{l}f({x_0})=1\\ f'({x_0})=0\end{array}\right.$.得到f(x)在x=x0处的导数等于0;
(ii)由(I)知x0=a.且f(x)在(a-1,a)内单调递增,在(a,a+1)内单调递减,故当x0=a时,f(x)≤f(a)=1在[a-1,a+1]上恒成立,从而g(x)≤ex在[x0-1,x0+1]上恒成立.由f(a)=a3-6a2-3a(a-4)a+b=1,得b=2a3-6a2+1,-1≤a≤1.构造函数t(x)=2x3-6x2+1,x∈[-1,1],利用导数求其值域可得b的范围.
解答 (Ⅰ)解:由f(x)=x3-6x2-3a(a-4)x+b,可得f'(x)=3x2-12x-3a(a-4)=3(x-a)(x-(4-a)),
令f'(x)=0,解得x=a,或x=4-a.由|a|≤1,得a<4-a.
当x变化时,f'(x),f(x)的变化情况如下表:
| x | (-∞,a) | (a,4-a) | (4-a,+∞) |
| f'(x) | + | - | + |
| f(x) | ↗ | ↘ | ↗ |
点评 本题考查利用导数研究函数的单调性,考查了利用研究过曲线上某点处的切线方程,训练了恒成立问题的求解方法,体现了数学转化思想方法,是压轴题.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:选择题
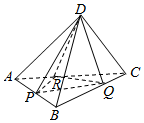 如图,已知正四面体D-ABC(所有棱长均相等的三棱锥),P、Q、R分别为AB、BC、CA上的点,AP=PB,$\frac{BQ}{QC}$=$\frac{CR}{RA}$=2,分别记二面角D-PR-Q,D-PQ-R,D-QR-P的平面角为α、β、γ,则( )
如图,已知正四面体D-ABC(所有棱长均相等的三棱锥),P、Q、R分别为AB、BC、CA上的点,AP=PB,$\frac{BQ}{QC}$=$\frac{CR}{RA}$=2,分别记二面角D-PR-Q,D-PQ-R,D-QR-P的平面角为α、β、γ,则( )| A. | γ<α<β | B. | α<γ<β | C. | α<β<γ | D. | β<γ<α |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {1,2,4} | C. | {1,2,4,6} | D. | {1,2,3,4,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com