
分析 (1)由∠C为钝角便可得到cosC<0,从而根据余弦定理便可得到$\frac{4+9-{x}^{2}}{12}<0$,解该不等式即可得出x的范围;
(2)可知a2+b2≥2ab,从而由a2+b2-ab=4便可得到ab≤4,又知道∠C=30°,从而由三角形的面积公式即可求出△ABC的面积S的范围,即可得出△ABC的面积S的最大值.
解答 解:(1)在△ABC中,∵∠C为钝角,
∴由余弦定理得,$cosC=\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}=\frac{4+9-{x}^{2}}{12}<0$;
∵x>0,∴解得$x>\sqrt{13}$;
又x<2+3;
∴x的范围为$(\sqrt{13},5)$;
(2)由a2+b2-ab=4得a2+b2=ab+4≥2ab,当a=b时取“=”;
∴ab≤4;
又∠C=30°;
∴${S}_{△ABC}=\frac{1}{2}absin30°=\frac{ab}{4}≤1$;
∴△ABC的面积S的最大值为1.
点评 考查钝角的余弦值小于0,余弦定理,以及不等式a2+b2≥2ab的运用,三角形的面积公式,不等式的性质.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
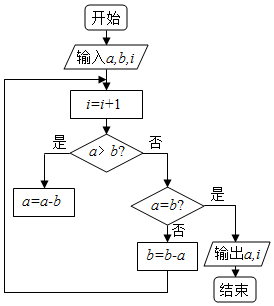 如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为12,16,0,则输出a和i的值分别为( )
如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为12,16,0,则输出a和i的值分别为( )| A. | 4,3 | B. | 4,4 | C. | 4,5 | D. | 3,4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
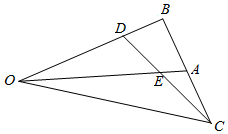 如图:已知,在△OAB中,点A是BC的中点,点D是将向量$\overrightarrow{OB}$分为2:1的一个分点,DC和OA交于点E,则AO与OE的比值是( )
如图:已知,在△OAB中,点A是BC的中点,点D是将向量$\overrightarrow{OB}$分为2:1的一个分点,DC和OA交于点E,则AO与OE的比值是( )| A. | 2 | B. | $\frac{5}{4}$ | C. | $\frac{3}{2}$ | D. | $\frac{6}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
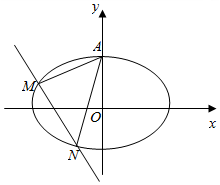 过椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1的上顶点A作斜率分别为k1,k2(k1,k2>0,k1≠k2)的两条直线l1,l2,它们分别与椭圆交于另一点M,N.
过椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1的上顶点A作斜率分别为k1,k2(k1,k2>0,k1≠k2)的两条直线l1,l2,它们分别与椭圆交于另一点M,N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | -$\frac{4}{3}$ | C. | -$\frac{2}{3}$ | D. | -3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com