
【题目】根据以往统计资料,某地车主购买甲种保险的概率为0.5,购买乙种保险但不购买甲种保险的概率为0.3.设各车主购买保险相互独立.
(1)求该地1位车主至少购买甲、乙两种保险中的1种的概率;
(2)X表示该地的100位车主中,甲、乙两种保险都不购买的车主数,求X的均值和方差.
【答案】(1)0.8;(2)E(X)=20,D(X)=16.
【解析】
(1)根据题意分别记事件,并得到各事件的概率,并根据事件间的关系,可得结果.
(2)根据(1)的条件,得到“甲、乙两种保险都不购买”的概率,根据X~B(100,0.2),利用公式直接可得结果.
设事件A表示“该地的1位车主购买甲种保险”,
事件B表示“该地的1位车主购买乙种保险但不购买甲种保险”,
事件C表示“该地的1位车主至少购买甲、乙两种保险中的1种”,
事件D表示“该地的1位车主甲、乙两种保险都不购买”,
(1)由题意知P(A)=0.5,P(B)=0.3,C=A∪B,
则P(C)=P(A∪B)=P(A)+P(B)=0.8.
(2)D=![]() ,P(D)=1-P(C)=1-0.8=0.2.
,P(D)=1-P(C)=1-0.8=0.2.
由题意知X~B(100,0.2),
所以均值E(X)=100×0.2=20,方差D(X)=100×0.2×0.8=16


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 是某城市的一个区域的示意图,阴影部分为街道,各相邻的两红绿灯之间的距离相等,
是某城市的一个区域的示意图,阴影部分为街道,各相邻的两红绿灯之间的距离相等,![]() 处为红绿灯路口,红绿灯统一设置如下:先直行绿灯30秒,再左转绿灯30秒,然后是红灯1分钟,右转不受红绿灯影响,这样独立的循环运行.小明上学需沿街道从
处为红绿灯路口,红绿灯统一设置如下:先直行绿灯30秒,再左转绿灯30秒,然后是红灯1分钟,右转不受红绿灯影响,这样独立的循环运行.小明上学需沿街道从![]() 处骑行到
处骑行到![]() 处(不考虑
处(不考虑![]() 处的红绿灯),出发时的两条路线(
处的红绿灯),出发时的两条路线(![]() )等可能选择,且总是走最近路线.
)等可能选择,且总是走最近路线.
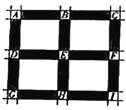
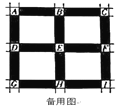
(1)请问小明上学的路线有多少种不同可能?
(2)在保证通过红绿灯路口用时最短的前提下,小明优先直行,求小明骑行途中恰好经过![]() 处,且全程不等红绿灯的概率;
处,且全程不等红绿灯的概率;
(3)请你根据每条可能的路线中等红绿灯的次数的均值,为小明设计一条最佳的上学路线,且应尽量避开哪条路线?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第41届世界博览会于2010年5月1日至10月31日,在中国上海举行,气势磅礴的中国馆——“东方之冠”令人印象深刻,该馆以“东方之冠,鼎盛中华,天下粮仓,富庶百姓”为设计理念,代表中国文化的精神与气质.其形如冠盖,层叠出挑,制似斗拱.它有四根高33.3米的方柱,托起斗状的主体建筑,总高度为60.3米,上方的“斗冠”类似一个倒置的正四棱台,上底面边长是139.4米,下底面边长是69.9米,则“斗冠”的侧面与上底面的夹角约为( ).

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A. 设![]() ,则
,则![]() 为实数的充要条件是
为实数的充要条件是![]() 为共轭复数;
为共轭复数;
B. “直线![]() 与曲线C相切”是“直线
与曲线C相切”是“直线![]() 与曲线C只有一个公共点”的充分不必要条件;
与曲线C只有一个公共点”的充分不必要条件;
C. “若两直线![]() ,则它们的斜率之积等于
,则它们的斜率之积等于![]() ”的逆命题;
”的逆命题;
D. ![]() 是R上的可导函数,“若
是R上的可导函数,“若![]() 是
是![]() 的极值点,则
的极值点,则![]() ”的否命题.
”的否命题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的两焦点与短轴两端点围成面积为12的正方形.
)的两焦点与短轴两端点围成面积为12的正方形.
(1)求椭圆C的标准方程;
(2)我们称圆心在椭圆上运动,半径为![]() 的圆是椭圆的“卫星圆”.过原点O作椭圆C的“卫星圆”的两条切线,分别交椭圆C于A、B两点,若直线
的圆是椭圆的“卫星圆”.过原点O作椭圆C的“卫星圆”的两条切线,分别交椭圆C于A、B两点,若直线![]() 、
、![]() 的斜率为
的斜率为![]() 、
、![]() ,当
,当![]() 时,求此时“卫星圆”的个数.
时,求此时“卫星圆”的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的图象为C,如下结论中正确的是( )
的图象为C,如下结论中正确的是( )
①图象C关于直线![]() 对称;②函数
对称;②函数![]() 在区间
在区间![]() 内是增函数;
内是增函数;
③图象C关于点![]() 对称;④由
对称;④由![]() 的图象向右平移
的图象向右平移![]() 个单位长度可以得到图象C
个单位长度可以得到图象C
A.①③B.②③C.①②③D.①②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com